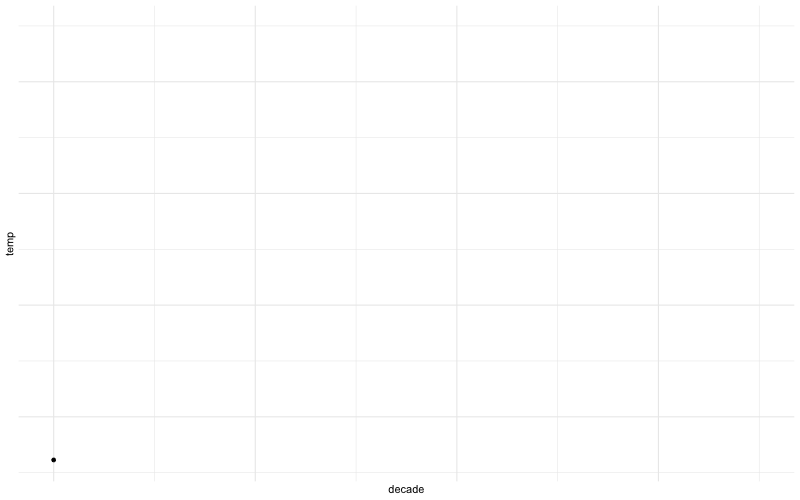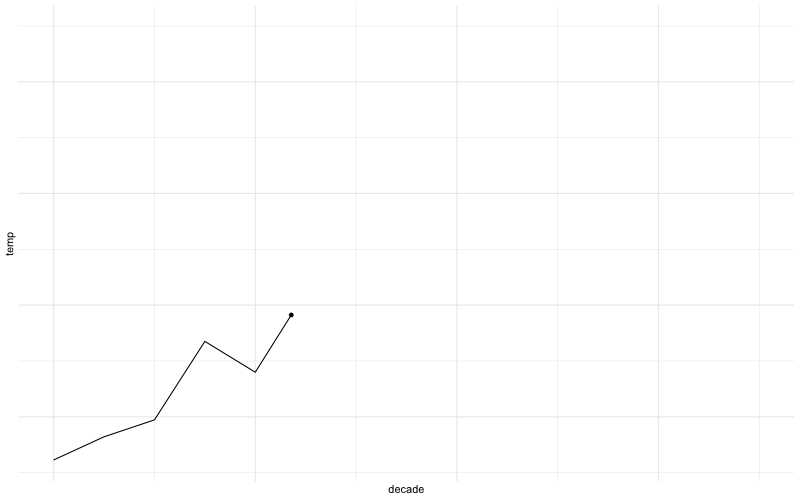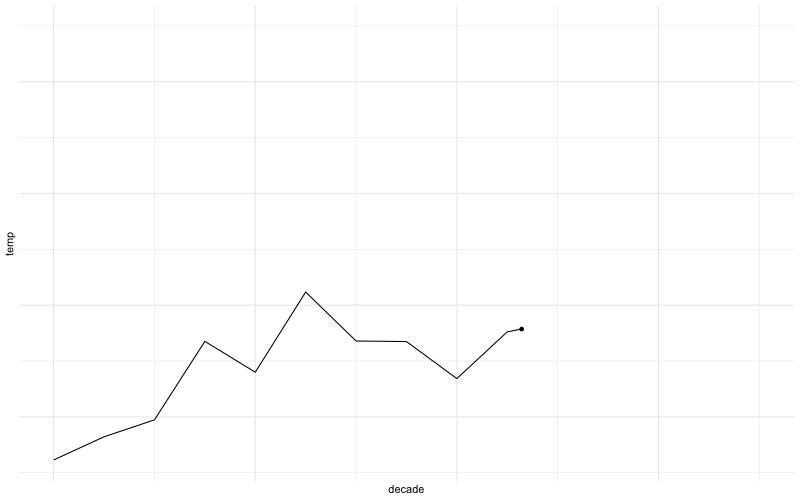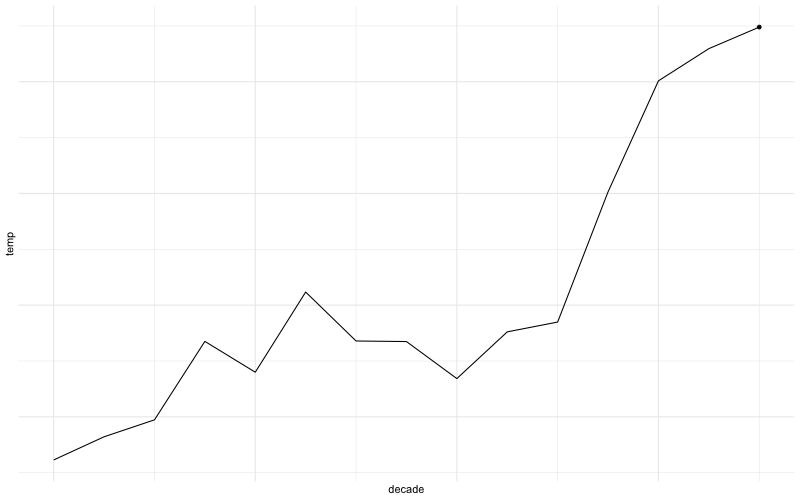10  Geradenmodelle 2

Schlüsselwörter

Statistik, Prognose, Modellierung, R, Datenanalyse, Regression

10.1 Einstieg

10.1.1 Lernziele

• Sie können Regressionsmodelle für Forschungsfragen mit binärer, nominaler und metrischer UV erläutern und in R anwenden.
• Sie können Interaktionseffekte in Regressionsmodellen erläutern und in R anwenden.
• Sie können den Anwendungszweck von Zentrieren und z-Transformationen zur besseren Interpretation von Regressionsmodellen erläutern und in R anwenden.

10.1.2 Benötigte R-Pakete

Neben den üblichen Paketen tidyverse (Wickham et al., 2019) und easystats (Lüdecke et al., 2022) benötigen Sie in diesem Kapitel noch yardstick (Kuhn et al., 2024) und optional ggpubr (Kassambara, 2023).

library(tidyverse)
library(yardstick)  # für Modellgüte im Test-Sample
library(easystats)
library(ggpubr)  # Daten visualisieren, optional

$$$$

10.1.3 Benötigte Daten

Dieses Mal arbeiten wir nicht nur mit den Mariokartdaten, sondern auch mit Wetterdaten.

mariokart_path <- "https://vincentarelbundock.github.io/Rdatasets/csv/openintro/mariokart.csv"
mariokart <- read.csv(mariokart_path)

wetter_path <- paste0(
  "https://raw.githubusercontent.com/sebastiansauer/",
  "statistik1/main/data/wetter-dwd/precip_temp_DWD.csv")
wetter <- read.csv(wetter_path)

Die Wetterdaten stammen vom DWD (2025a, 2025b) Ein Data-Dictionary für den Datensatz können Sie hier herunterladen.

10.2 Forschungsbezug: Gläserne Kunden

Lineare Modelle (synonym: Regressionsanalysen) sind ein altes, aber mächtiges Werkzeug. Sie gehören immer noch zum Standard-Repertoire moderner Analystinnen und Analysten. Die Wirkmächtigkeit von linearen Modellen zeigt sich (leider?!) in folgendem Beispiel.

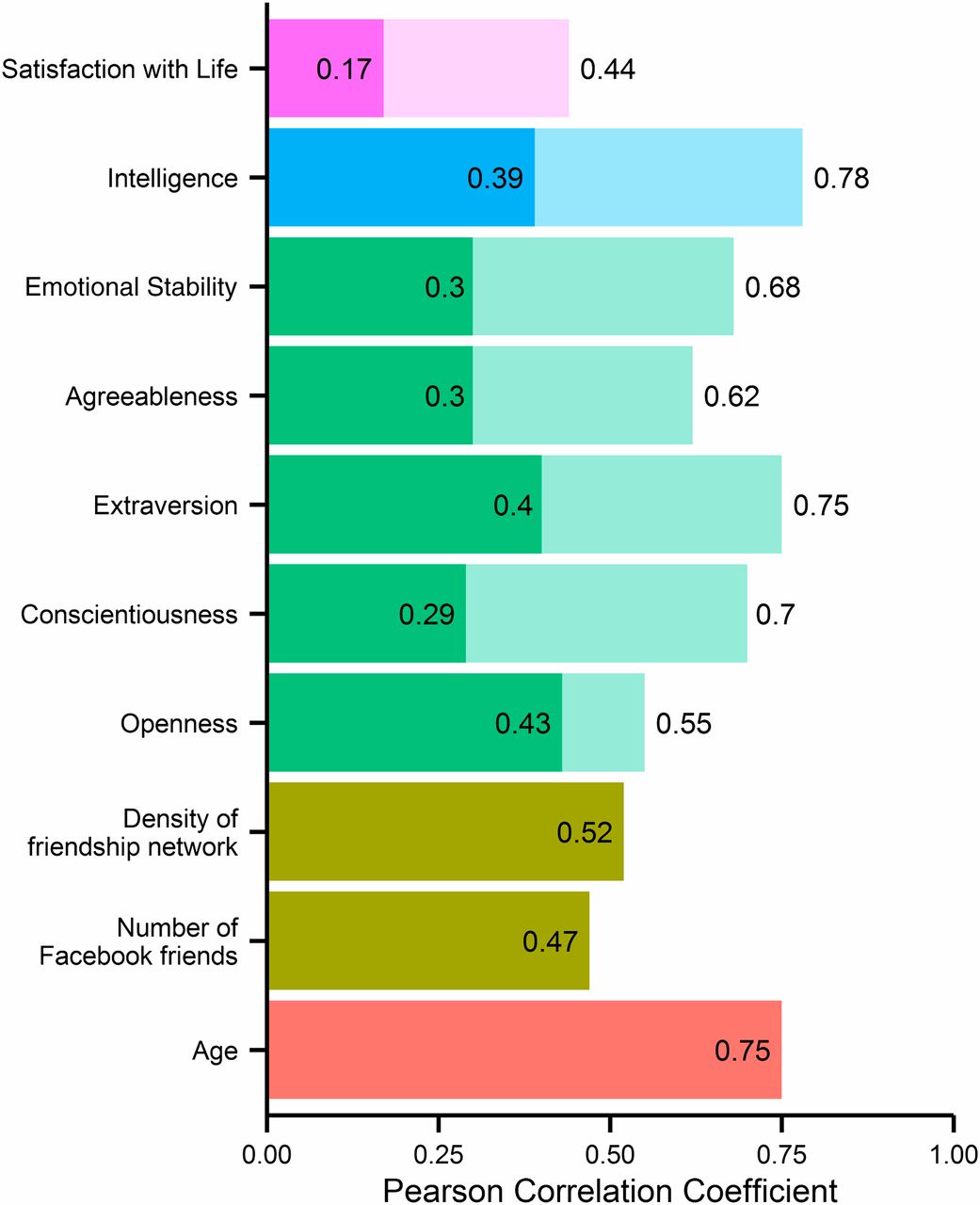
Beispiel 10.1 (Wie gut kann man Ihre Persönlichkeit auf Basis Ihrer Social-Media-Posts vorhersagen?) In einer Studie mit viel Medienresonanz untersuchten Kosinski et al. (2013), wie gut Persönlichkeitszüge durch Facebook-Daten (Likes etc.) vorhergesagt werden können. Die Autoren resümieren im Abstract:

We show that easily accessible digital records of behavior, Facebook Likes, can be used to automatically and accurately predict a range of highly sensitive personal attributes including: sexual orientation, ethnicity, religious and political views, personality traits, intelligence, happiness, use of addictive substances, parental separation, age, and gender.

Die Autoren berichten über eine hohe Modellgüte (gemessen mit dem Korrelationskoeffizienten $r$) zwischen den tatsächlichen persönlichen Attributen und den vorhergesagten Werten Ihres Modells, s. Abbildung 10.1. Das eingesetzte statistische Modell beruht auf einem linearen Modell, also ähnlich den in diesem Kapitel vorgestellten Methoden. Neben der analytischen Stärke der Regressionsanalyse zeigt das Beispiel auch, wie gläsern man im Internet ist! $◻$

Abbildung 10.1: Prediction accuracy of regression for numeric attributes and traits expressed by the Pearson correlation coefficient between predicted and actual attribute values (Kosinski et al., 2013)

10.3 Wetter in Deutschland

Beispiel 10.2 (Wetterdaten) Nachdem Sie einige Zeit als Datenanalyst bei dem Online-Auktionshaus gearbeitet haben, stand Ihnen der Sinn nach etwas Abwechslung. Viel Geld verdienen ist ja schon ganz nett, aber dann fiel Ihnen ein, dass Sie ja zu Generation Z gehören, und daher den schnöden Mammon nicht so hoch schätzen sollten. Sie entschließen sich, Ihre hochgeschätzten Analyse-Skills für etwas einzusetzen, das Ihnen sinnvoll erscheint: Die Analyse des Klimawandels. $◻$

Beim Deutschen Wetterdienst, DWD, haben Sie sich Wetterdaten von Deutschland heruntergeladen. Nach etwas Datenjudo, auf das wir hier nicht eingehen wollen, resultiert ein schöner Datensatz, den Sie jetzt analysieren möchten. (Im Datensatz ist die Temperatur ist in Grad Celsius angegeben; der Niederschlag (precip) in mm Niederschlag pro Quadratmeter.) Hervorragend! An die Arbeit!

Abbildung 10.2 zeigen die Wetterdaten animiert.

Temperaturverlauf

Temperatur (Grad Celsius) im Verlauf der Jahre

Niederschlagsverlauf

Niederschlag (mm) im Verlauf der Jahre

Monatstemperaturverlauf

Veränderung der Temperatur pro Monat in Deutschland im Zeitverlauf (10-Jahres-Mittelwerte

Abbildung 10.2: Veränderung der Temperatur und Niederschlag (10-Jahres-Mittel) in Deutschland im Verlauf des 20. Jahrhunderts

10.3.1 Metrische UV

In diesem Abschnitt untersuchen wir lineare Modelle mit einer oder mehreren metrischen UV (und einer metrischen AV).

Sie stellen sich nun folgende Forschungsfrage:

🧑‍🏫 Um wieviel ist die Temperatur in Deutschland pro Jahr gestiegen, wenn man die letzten ca. 100 Jahre betrachtet?

Die Modellparameter von lm_wetter1 sind in Tabelle 10.1 zu sehen.

lm_wetter1 <- lm(temp ~ year, data = wetter)
parameters(lm_wetter1)

Tabelle 10.1: Modellparameter von lm_wetter1

Fixed Effects

Parameter	Coefficient	CI
(Intercept)	-14.25	(-17.87, -10.63)
year	0.01	(9.80e-03, 0.01)

Laut dem Modell wurde es pro Jahr im Schnitt um 0.01$$°C wärmer, pro Jahrzehnt also 0.1$$°C und pro Jahrhundert 1$$°C.

🧑‍🎓 Das ist sicherlich nicht linear! Vermutlich ist die Temperatur bis 1950 konstant geblieben und jetzt knallt sie durch die Decke!

🧑‍🏫 Mit der Ruhe, das schauen wir uns später an.

In Tabelle 10.1 finden sich zwei Arten von Information für den Wert des Achsenabschnitts (${\beta }_0$) und des Regressionsgewichts von year (${\beta }_1$):

1. Punktschätzungen In der Spalte Coefficient sehen Sie den “Best-Guess” (Punktschätzer) für den entsprechenden Koeffizienten in der Population. Das ist sozusagen der Wert, für den sich das Modell festlegen würde, wenn es sonst nichts sagen dürfte.

2. Bereichschätzungen Cleverer als Punktschätzungen sind Bereichsschätzungen (Intervallschätzungen): Hier wird ein Bereich plausibler Werte für den entsprechenden Koeffizienten angegeben. In der Spalte CI sehen Sie die untere bzw. die obere Grenze eines “Bereichs plausibler Werte”. Dieser Schätzbereich wird auch als Konfidenzintervall (engl. confidence interval, CI) bezeichnet. Ein Konfidenzintervall ist mit einer Sicherheit zwischen 0 und 1 angegeben, z.B. 95$$% (0.95). Grob gesagt bedeutet ein 95$$%-Kondidenzintervall, dass wir uns (laut Modell) zu 95$$% sicher sein können, dass der wahre Werte sich in diesem Bereich befindet. In Tabelle 10.1 können wir ablesen, dass das Regressionsgewicht von year irgendwo zwischen praktisch Null (0.009) und ca. 0.01 Grad geschätzt wird. Je schmaler das Konfidenzintervall, desto genauer wird der Effekt geschätzt (unter sonst gleichen Umständen).

Definition 10.1 (Konfidenzintervall) Ein Konfidenzintervall (confidence interval, CI) gibt einen Schätzbereich plausibler Werte für einen Populationswert an, auf Basis der Schätzung, die uns die Stichprobe liefert. $◻$

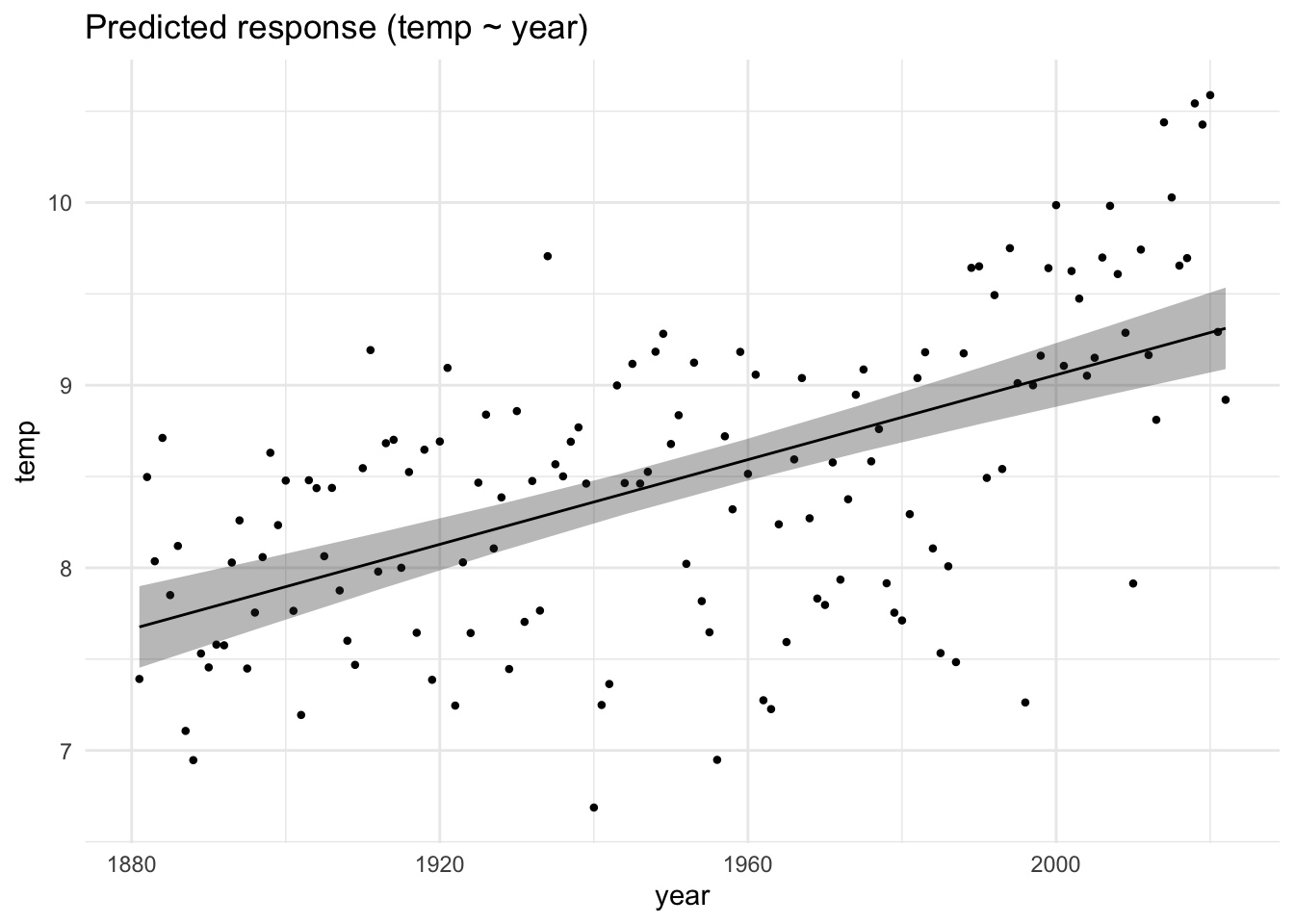
Das Modell lm_wetter1, bzw. die Schätzungen zu den erwarteten Werten, kann mich sich so ausgeben lassen, s. Abbildung 10.3, links. Allerdings sind das zu viele Datenpunkte. Wir sollten es vielleicht anders visualisieren, s. Abbildung 10.3, rechts. Dazu aggregieren wir die Messwerte eines Jahres zu jeweils einem Mittelwert. Auf dieser Basis erstellen wir ein neues lineares Modell, lm_wetter1_pro_jahr, s. Tabelle 10.2.

wetter_summ <-
  wetter %>% 
  group_by(year) %>% 
  summarise(temp = mean(temp),
            precip = mean(precip))  # precipitation: engl. für Niederschlag

# Summierte Daten (nach Jahr), aber gleiche Modellformel:
lm_wetter1_pro_jahr <- lm(temp ~ year, data = wetter_summ) 
parameters(lm_wetter1_pro_jahr) |> 
  select(Parameter, Coefficient)

Tabelle 10.2: Modellparameter von lm_wetter1a

Fixed Effects

Parameter	Coefficient
(Intercept)	-14.14
year	0.01

Komfortabel ist es, das Modell lm_wetter1_pro_jahr mit plot(estimate_relation(lm_wetter1_pro_jahr)) zu plotten.

(a) Ein Punkt pro Tag

 

(b) Ein Punkt pro Jahr

Abbildung 10.3: Die Veränderung der mittleren Temperatur in Deutschland im Zeitverlauf [DWD2025]. Links: Jeder Punkt ist ein Tag (viel Overplotting, wenig nützlich). Rechts: Jeder Punkt ist ein Jahr (wetter_summ). Außerdem ist die Regressionsgerade dargestellt.

🧑‍🎓 Moment mal, der Achsenabschnitt liegt bei etwa -14 Grad! Was soll das bitte bedeuten?

10.3.2 UV zentrieren

Zur Erinnerung: Der Achsenabschnitt (${\beta }_0$; engl. intercept) ist definiert als der $Y$-Wert an der Stelle $x=0$, s. Kapitel 9.5.

In den Wetterdaten wäre Jahr=0 Christi Geburt. Da unsere Wetteraufzeichnung gerade mal ca. 150 Jahre in die Vergangenheit reicht, ist es vollkommen vermessen, dass Modell 2000 Jahre in die Vergangenheit zu extrapolieren, ganz ohne, dass wir dafür Daten haben, s. https://xkcd.com/605/. Sinnvoller ist es da, z.$$B. einen Referenzwert festzulegen, etwa 1950. Wenn wir dann von allen Jahren 1950 abziehen, wird das Jahr 1950 zum neuen Jahr Null. Damit bezöge sich der Achsenabschnitt auf das Jahr 1950, was Sinn macht, denn für dieses Jahr haben wir Daten. Hat man nicht einen bestimmten Wert, der sich als Referenzwert anbietet, so ist es nützlich den Mittelwert (der UV) als Referenzwert zu nehmen. Diese Transformation bezeichnet man als Zentrierung (engl. centering) der Daten, s. Definition 7.7 und Listing 7.3.

Abbildung 10.4: Du sollst nicht ein Modell weit außerhalb seines Datenbereichs extrapolieren

wetter <-
  wetter %>% 
  mutate(year_c = year - mean(year))  # "c" wie centered

Das mittlere Jahr in unserer Messwertereihe ist übrigens 1951, wie etas Datenjudo zeigt: wetter %>% summarise(mean(year))

Die Steigung (d.$$h. der Regressionskoeffizient für year_c) bleibt durch das Zentrieren unverändert, nur der Achsenabschnitt ändert sich, s. Tabelle 10.3.

lm_wetter1_zentriert <- lm(temp ~ year_c, data = wetter)
parameters(lm_wetter1_zentriert) |> 
  select(Coefficient, Parameter, CI_low, CI_high)

Tabelle 10.3: Modellparameter von lm_wetter1_zentriert

Fixed Effects

Coefficient	Parameter	CI
8.49	(Intercept)	(8.42, 8.57)
0.01	year_c	(9.80e-03, 0.01)

Jetzt ist die Interpretation des Achsenabschnitts komfortabel: Im Jahr 1951 (x=0) lag die mittlere Temperatur in Deutschland (laut DWD) bei ca. 8.5$$°C. Die Regressionsgleichung lautet: temp_pred = 8.49 + 0.01*year_c. In Worten: Wir sagen eine Temperatur vorher, die sich als Summe von 8.49$$°C plus 0.01 mal das Jahr (in zentrierter Form) berechnet.

Wie gut erklärt unser Modell die Daten?

r2(lm_wetter1_zentriert)  # aus `{easystats}`
## # R2 for Linear Regression
##        R2: 0.005
##   adj. R2: 0.005

Viel Varianz des Wetters erklärt das Modell mit year_c aber nicht. (year und year_c sind gleich stark mit temp korreliert, daher wird sich die Modellgüte nicht unterscheiden.). Macht auch Sinn: Abgesehen von der Jahreszahl spielt z.$$B. die Jahreszeit eine große Rolle für die Temperatur. Das haben wir nicht berücksichtigt.

🧑‍🎓 Wie warm ist es laut unserem Modell dann im Jahr 2051?

predict(lm_wetter1_zentriert, newdata = tibble(year_c = 100))
##   1 
## 9.7

🧑‍🎓 Moment! Die Vorhersage ist doch Quatsch! Schon im Jahr 2022 lag die Durchschnittstemperatur bei 10,5° Celsius (Wilke, 2013).

🧑‍🏫 Wir brauchen ein besseres Modell! Zum Glück haben wir ambitionierten Wissenschaftsnachwuchs.

Die Veränderung der auf fünf Jahre gemittelten Abweichung der Lufttemperatur zum Mittel von von 1951 bis 1980 ist in Abbildung 10.5 dargestellt. Links ist eine grobe Temperaturrasterung zu sehen (Daten ab 1753)¹; rechts eine feinere (Daten ab 1881)².

Temperaturverlauf in Deutschland von 1753 bis 2020 (Habitator terrae, 2021)

Abbildung 10.5:

10.3.3 Binäre UV

Definition 10.2 (Binäre Variable) Eine binäre UV, auch Indikatorvariable oder Dummyvariable genannt, hat nur zwei Ausprägungen: 0 und 1. $◻$

Beispiel 10.3 (Binäre Variablen) Das sind zum Beispiel weiblich mit den Ausprägungen 0 (nein) und 1 (ja) oder before_1950 mit 1 für Jahre früher als 1950 und 0 ansonsten. $◻$

Beispiel 10.4 Hier interessiert Sie folgende Forschungsfrage:

🧑‍🎓 Ob es in der zweiten Hälfte des 20. Jahrhunderts wohl wärmer war, im Durchschnitt, als vorher? $◻$

Aber wie erstellen Sie eine Variable after_1950, um die zweite Hälfte des 20. Jahrhunderts (und danach) zu fassen? Nach einigem Überlegen kommen Sie auf die Idee, das vektorisierte Rechnen von R (s. Kapitel 3.6.5) auszunutzen:

year <- c(1940, 1950, 1960)
after_1950 <- year > 1950  # prüfe, ob as Jahr größer als 1950 ist
after_1950
## [1] FALSE FALSE  TRUE

Die ersten zwei Jahre von year sind nicht größer als 1950, das dritte schon. Ja, so könnte das klappen! Diese Syntax übertragen Sie auf Ihre wetter-Daten:

wetter <-
  wetter %>% 
  mutate(after_1950 = year > 1950) %>% 
  filter(region != "Deutschland")  # ohne Daten für Gesamt-Deutschland

Scheint zu klappen! Jetzt ein lineares Modell dazu berechnen, s. Tabelle 10.4.

lm_wetter_bin_uv <- lm(temp ~ after_1950, data = wetter)

Tabelle 10.4: Parameter von lm_wetter_bin_uv

Fixed Effects

Parameter	Coefficient	CI
(Intercept)	8.18	(8.06, 8.29)
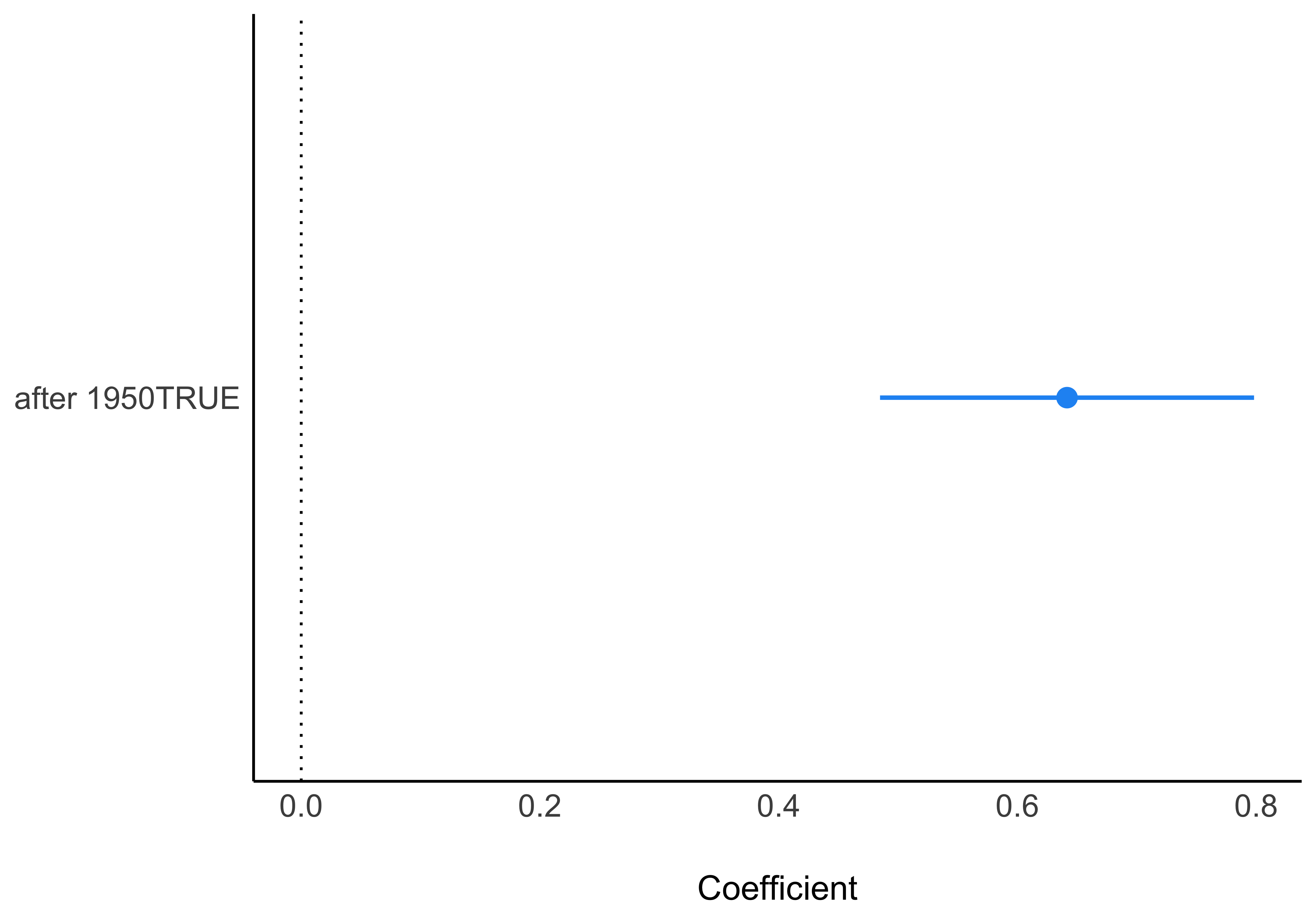
after_1950TRUE	0.64	(0.48, 0.80)

Die Parameterwerte des Modells lassen darauf schließen, dass es tatsächlich wärmer geworden ist nach 1950, und zwar offenbar ein gutes halbes Grad, s. Abbildung 10.6.

(a) Mittelwertsunterschied als Regressionsparameter

 

(b) Mittelwertsunterschied als Verteilungsvergleich

Abbildung 10.6: Modell: temp ~ after_1950, (a) Der Schätzbereich für den Parameter reicht von ca. 0.5 bis 0.8 Grad Unterschied. (b) Der Unterschied sieht in dieser Darstellung nicht groß aus.

Leider zeigt ein Blick zum Ergebnis der Funktion r2, dass die Vorhersagegüte des Modells zu wünschen übrig lässt (r2(lm_wetter_bin_uv)). Wir brauchen ein besseres Modell.

Um die Koeffizienten eines linearen Modells auszurechnen, benötigt man eine metrische UV und eine metrische AV. Hier haben wir aber keine richtige metrische UV, sondern eine logische Variable mit den Werten TRUE und FALSE. Um die UV in eine metrische Variable umzuwandeln, gibt es einen einfachen Trick, den R für uns ohne viel Ankündigung durchführt: Umwandling in eine oder mehrere binäre Variablen, s. Definition 10.2.

Hat eine nominale UV zwei Stufen, so überführt (synonym: transformiert) lm diese Variable in eine binäre Variable. Da eine binäre Variable wie eine metrische angesehen werden kann, kann die Regression in gewohnter Weise durchgeführt werden. Wenn Sie die Ausgabe der Parameter betrachten, so sehen Sie die neu erstellte binäre Variable (s. Tabelle 10.4). Man beachte, dass der ursprüngliche Datensatz nicht geändert wird, nur während der Analyse von lm wird die Umwandlung der Variable durchgeführt.

In unserem Fall liegt mit after_1950 eine logische Variable mit den Werten TRUE und FALSE vor. TRUE und FALSE werden von R automatisch als 1 bzw. als 0 verstanden. Also: Eine logische Variable ist schon eine binäre Variable.

🤖 Eine 1 kannst du als “Ja! Richtig!” verstehen und eine 0 als “Nein! Falsch!”

Beispiel 10.5 (Beispiel: ‘Geschlecht’ in eine binäre Variable umwandeln.) Angenommen wir haben eine Variable geschlecht mit den zwei Stufen Frau und Mann und wollen diese in eine Indikatorvariable umwandeln. Da “Frau” alphabetisch vor “Mann” kommt, nimmt R “Frau” als erste Stufe bzw. als Referenzgruppe. “Mann” ist dann die zweite Stufe, die in der Regression dann in Bezug zur Referenzgruppe gesetzt wird. lm wandelt uns diese Variable in geschlechtMann um mit den zwei Stufen 0 (kein Mann, also Frau) und 1 (Mann). $◻$

id	geschlecht
1	Mann
2	Frau

$\to$

id	geschlechtMann
1	1
2	0

Wichtig

Ein lineares Modell mit binärer UV zeigt nichts anderes als die Differenz der Gruppenmittelwerte. $◻$

wetter %>% 
  group_by(after_1950) %>% 
  summarise(temp_mean = mean(temp))

after_1950	temp_mean
FALSE	8.2
TRUE	8.8

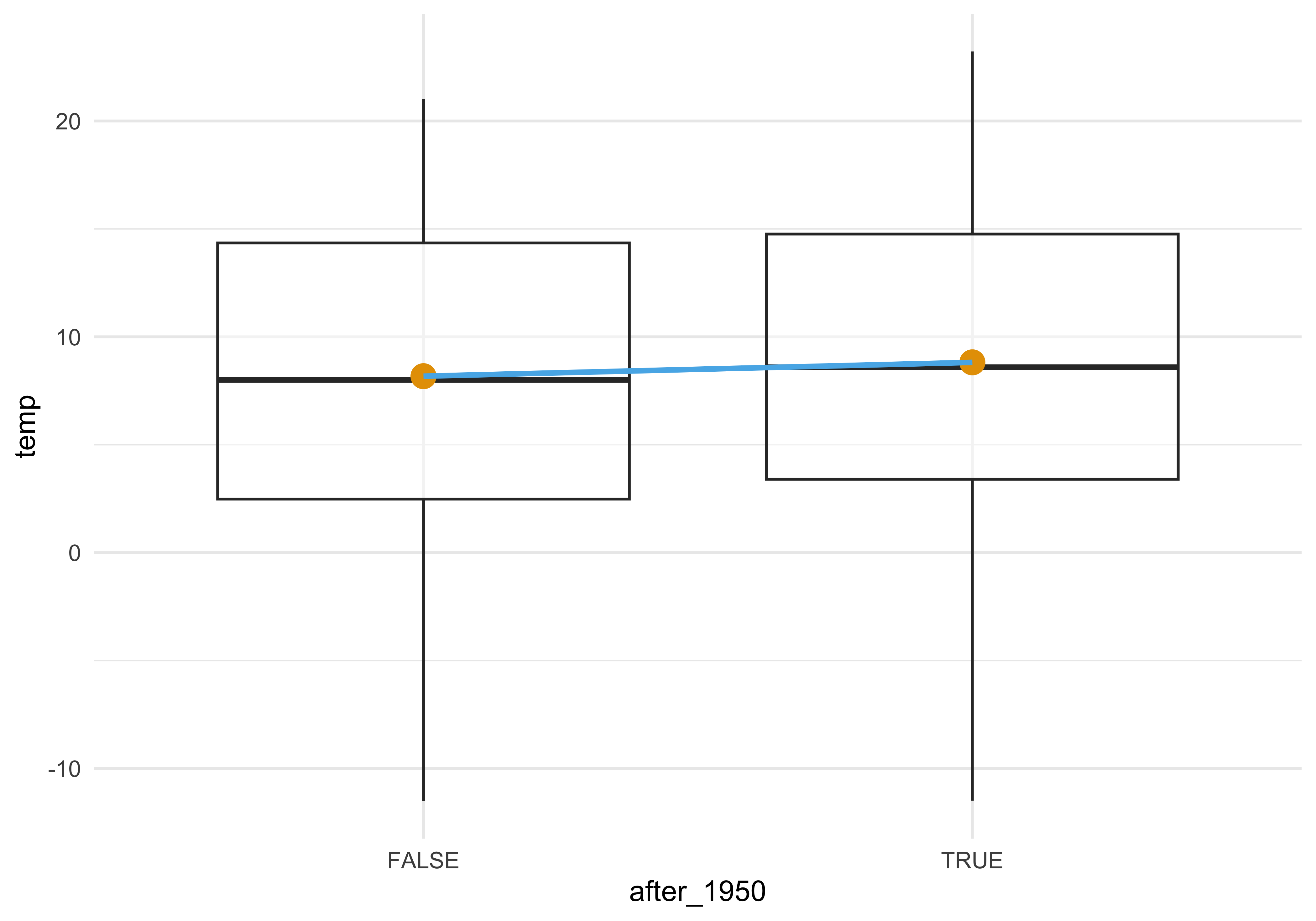
Die Interpretation eines linearen Modells mit binärer UV veranschaulicht Abbildung 10.7: Der Achsenabschnitt (${\beta }_0$) entspricht dem Mittelwert der 1. Gruppe. Der Mittelwert der 2. Gruppe entspricht der Summe aus Achsenabschnitt und dem Koeffizienten der zweiten Gruppe. (Abbildung 10.7 zeigt nur die Daten für den Monat Juli im Bundesland Bayern, der Einfachheit und Übersichtlichkeit halber.)

Abbildung 10.7: Sinnbild zur Interpretation eines linearen Modells mit binärer UV (reingezoomt, um den Mittelwertsunterschied hervorzuheben)

Fassen wir die Interpretation der Koeffizienten für das Modell mit binärer UV zusammen:

1. Mittelwert der 1. Gruppe (bis 1950): Achsenabschnitt (${\beta }_0$)
2. Mittelwert der 2. Gruppe (nach 1950): Achsenabschnitt (${\beta }_0$) + Steigung der Regressionsgeraden (${\beta }_1$)

Für die Modellwerte $\hat{y}$ gilt also:

• Temperatur laut Modell bis 1950: $\hat{y}={\beta }_0=17.7$

• Temperatur laut Modell bis 1950: $\hat{y}={\beta }_0+{\beta }_1=17.7+0.6=18.3$

Bei nominalen (und auch bei binären) Variablen kann man ${\beta }_1$ als einen Schalter verstehen; bei metrischen Variablen als einen Dimmer.³ $◻$

10.3.4 Nominale UV

In diesem Abschnitt betrachten wir ein lineares Modell (für uns synonym: Regressionsmodell) mit einer mehrstufigen (nominalskalierten) UV. So ein Modell ist von den Ergebnissen her praktisch identisch zu einer Varianzanalyse mit einer einzigen UV.

Beispiel 10.6 Ob es wohl substanzielle Temperaturunterschiede zwischen den Bundesländern gibt?

Befragen wir dazu ein lineares Modell; in Tabelle 10.5 sind für jeden Parameter der Punktschätzer (Koeffizient) und der zugehörige Schätzbereich (Konfidenzintervall) mit Ober- und Untergrenze angegeben.

lm_wetter_region <- lm(temp ~ region, data = wetter)

Tabelle 10.5: Modellparameter für lm_wetter_region

Fixed Effects

Parameter	Coefficient	CI
(Intercept)	8.25	(7.93, 8.56)
regionBayern	-0.63	(-1.07, -0.19)
regionBrandenburg	0.57	(0.13, 1.02)
regionBrandenburg/Berlin	0.58	(0.14, 1.03)
regionHessen	0.11	(-0.33, 0.56)
regionMecklenburg-Vorpommern	0.08	(-0.37, 0.52)
regionNiedersachsen	0.52	(0.07, 0.96)
regionNiedersachsen/Hamburg/Bremen	0.52	(0.08, 0.96)
regionNordrhein-Westfalen	0.80	(0.35, 1.24)
regionRheinland-Pfalz	0.46	(0.02, 0.90)
regionSaarland	0.71	(0.27, 1.16)
regionSachsen	-0.04	(-0.48, 0.40)
regionSachsen-Anhalt	0.55	(0.11, 1.00)
regionSchleswig-Holstein	0.17	(-0.27, 0.62)
regionThueringen	-0.48	(-0.92, -0.03)
regionThueringen/Sachsen-Anhalt	0.10	(-0.34, 0.54)

Hat die nominalskalierte UV mehr als zwei Stufen, so transformiert lm sie in mehr als eine Indikatorvariable um. Genauer gesagt ist es immer eine Indikatorvariable weniger als es Stufen in der nominalskalierten Variablen gibt. Allgemein gilt: Hat eine nominale Variable $k$ Stufen, so wird diese Variable von lm in $k-1$ binäre Variablen umgewandelt.

Betrachten wir ein einfaches Beispiel, eine Tabelle mit der Spalte Bundesland – aus Gründen der Einfachheit hier nur mit drei Bundesländern. Damit lm arbeiten kann, wird Bundesland in zwei Indikatorvariablen umgewandelt.

id	Bundesland
1	BaWü
2	Bayern
3	Brandenburg

$\to$

id	BL_Bayern	BL_Bra
1	0	0
2	1	0
3	0	1

Auch im Fall mehrerer Ausprägungen einer nominalen Variablen gilt die gleiche Logik der Interpretation wie bei binären Variablen:

1. Mittelwert der 1. Gruppe: Achsenabschnitt (${\beta }_0$)
2. Mittelwert der 2. Gruppe: Achsenabschnitt (${\beta }_0$) + Steigung der 1. Regressionsgeraden (${\beta }_1$)
3. Mittelwert der 3. Gruppe: Achsenabschnitt (${\beta }_0$) + Steigung der 2. Regressionsgeraden (${\beta }_2$)
4. usw.

Es kann nervig sein, dass das Bundesland, welches als Referenzgruppe (sprich als Gruppe des Achsenabschnitts) ausgewählt wurde nicht explizit in der Ausgabe angegeben ist. Der Wert der Referenzgruppe findet seinen Niederschlag im Achsenabschnitt. Bei einer Variable vom Typ character wählt R den alphabetisch ersten Wert als Referenzgruppe für ein lineares Modell aus. Bei einer Variable vom Typ factor ist die Reihenfolge bereits festgelegt, vgl. Kapitel 10.3.5. Der Mittelwert dieser Gruppe entspricht dem Achsenabschnitt.

Beispiel 10.7 (Achsenabschnitt in wetter_lm2) Da Baden-Württemberg das alphabetisch erste Bundesland ist, wird es von R als Referenzgruppe ausgewählt, dessen Mittelwert als Achsenabschnitt im linearen Modell hergenommen wird. $◻$

Am einfachsten verdeutlicht sich lm_wetter_region vielleicht mit einem Diagramm, s. Abbildung 10.8.

Abbildung 10.8: Sinnbild zur Interpretation eines linearen Modells mit nominaler UV (reingezoomt, um den Mittelwertsunterschied hervorzuheben).

Beispiel 10.8 (Niederschlagsmenge im Vergleich der Monate) Eine weitere Forschungsfrage, die Sie nicht außer acht lassen wollen, ist die Frage nach den jahreszeitlichen Unterschieden im Niederschlag (engl. precipitation). Los R, rechne! $◻$

🤖 Endlich geht’s weiter! Ergebnisse findest du in Tabelle 10.6!

lm_wetter_month <- lm(precip ~ month, data = wetter)
parameters(lm_wetter_month)

Tabelle 10.6: Modellparameter für lm_wetter_month

Parameter	Coefficient	SE	95% CI	t(27166)	p
(Intercept)	53.27	0.41	(52.46, 54.08)	128.76	< .001
month	1.14	0.06	(1.03, 1.25)	20.29	< .001

Ja, da scheint es deutliche Unterschiede im Niederschlag zu geben. Wir brauchen ein Diagramm zur Verdeutlichung, s. Abbildung 10.9, links (plot(estimate_expectation(lm_wetter_month)). Oh nein: R betrachtet month als numerische Variable! Aber “Monat” bzw. “Jahreszeit” sollte nominal sein.

🤖 Aber month ist als Zahl in der Tabelle hinterlegt. Jede ehrliche Maschine verarbeitet eine Zahl als Zahl, ist doch klar!

👩 Okay, R, wir müssen month in eine nominale Variable transformieren. Wie geht das?

🤖 Dazu kannst du den Befehl factor nehmen. Damit wandelst du eine numerische Variable in eine nominalskalierte Variable (Faktorvariable) um. Faktisch heißt das, dass dann eine Zahl als Text gesehen wird.

Beispiel 10.9 Transformiert man 42 mit factor, so wird aus 42 "42". Aus der Zahl wird ein Text. Alle metrischen Eigenschaften gehen verloren; die Variable ist jetzt auf nominalen Niveau. $◻$

wetter <-
  wetter %>% 
  mutate(month_factor = factor(month))

Jetzt berechnen wir mit der faktorisierten Variablen ein lineares Modell, s. Tabelle 10.7.

lm_wetter_month_factor <- lm(precip ~ month_factor, data = wetter)
parameters(lm_wetter_month_factor) |> 
  select(Parameter, Coefficient)

Tabelle 10.7: Modellparameter von lm_wetter_month_factor (nur die ersten paar Parameter)

Parameter	Coefficient
(Intercept)	57.0
month_factor2	-9.9
month_factor3	-7.8
month_factor4	-8.5
month_factor5	4.7
month_factor6	14.3

Sehr schön! Jetzt haben wir eine Referenzgruppe (Monat 1, d.$$h. Januar) und 11 Unterschiede zum Januar, s. Abbildung 10.9.

Übungsaufgabe 10.1 In ähnlicher Form zu Abbildung 10.9 könnten Sie auch die Regressionsgewichte wie folgt plotten: parameters(lm_wetter_month_factor) |> plot(). Was sind die Unterschiede zu Abbildung 10.9?⁴ $◻$

ggerrorplot(data = wetter,
            x = "month_factor",
            y = "precip",
            desc_stat = "mean_sd")

Abbildung 10.9: Niederschlagsmengen nach Monaten (Mittelwerte plus SD)

Möchte man die Referenzgruppe eines Faktors ändern, kann man dies mit relevel tun:

wetter <-
  wetter %>% 
  mutate(month_factor = relevel(month_factor, ref = "7"))

So sieht dann die geänderte Reihenfolge aus:⁵

levels(wetter$month_factor)
##  [1] "7"  "1"  "2"  "3"  "4"  "5"  "6"  "8"  "9"  "10" "11" "12"

10.3.5 Binäre plus metrische UV

In diesem Abschnitt untersuchen wir ein lineares Modell mit zwei UV: einer zweistufigen (binären) UV plus einer metrischen UV. Ein solches Modell kann auch als Kovarianzanalyse (engl. analysis of covariance, ANCOVA) bezeichnet werden.

Beispiel 10.10 Ob sich die Niederschlagsmenge wohl unterschiedlich zwischen den Monaten entwickelt hat in den letzten gut 100 Jahren? Der Einfachheit halber greifen Sie sich nur zwei Monate heraus (Januar und Juli).

wetter_month_1_7 <-
  wetter %>% 
  filter(month == 1  | month == 7) 

🧑‍🏫 Ich muss mal kurz auf eine Sache hinweisen …

Eine Faktorvariable ist einer der beiden Datentypen in R, die sich für nominalskalierte Variablen anbieten: Textvariablen (character) und Faktor-Variablen (factor). Ein wichtiger Unterschied ist, dass die erlaubten Ausprägungen (“Faktorstufen”) bei einer Faktor-Variable mitgespeichert werden, bei der Text-Variable nicht. Das kann praktisch sein, denn bei einer Faktorvariable ist immer klar, welche Ausprägungen in Ihrer Variable möglich sind. $◻$

Beispiel 10.11 (Beispiele für Faktorvariablen)  

geschlecht <- c("f", "f", "m")
geschlecht_factor <- factor(geschlecht)
geschlecht_factor
## [1] f f m
## Levels: f m

Filtern verändert die Faktorstufen nicht. Wenn Sie von der Faktorvariablen⁶ geschlecht das 3. Element ("m") herausfiltern, so dass z.$$B. nur die ersten beiden Elemente übrig bleiben mit allein der Ausprägung "f", merkt sich R trotzdem, dass die Variable laut Definition zwei Faktorstufen besithzt ("f" und "m").

Genau so ist es, wenn Sie aus wetter nur die Monate "1" und "7" herausfiltern: R merkt sich, dass es 12 Faktorstufen gibt. Möchten Sie die herausgefilterten Faktorstufen “löschen”, so können Sie einfach die Faktorvariable neu definieren (mit factor).

wetter_month_1_7 <-
  wetter %>% 
  filter(month == 1  | month == 7) %>% 
  # Faktor (und damit die Faktorstufen) neu definieren:
  mutate(month_factor = factor(month))

Hat man mehrere (“multiple”) X-Variablen (Prädiktoren, unabhängige Variablen), so trennt man sich mit einem Plus-Zeichen in der Regressionsformel, z.$$B. temp ~ year_c + month.

Definition 10.3 (Multiple Regression) Eine multiple Regression beinhaltet mehr als eine X-Variable. Die Modellformel spezifiziert man so:

$y\sim x_1+x_2+\dots +x_n◻$

Die Veränderung der monatlichen Temperatur (10-Jahres-Mittel) ist in Abbildung 10.2, c) dargestellt (aber mit allen 12 Monaten, sieht schöner aus).

Das Pluszeichen hat in der Modellgleichung (synonym: Regressionsformel) keine arithmetische Funktion. Es wird nichts addiert. In der Modellgleichung sagt das Pluszeichen nur “und noch folgende UV …”.

Die Modellgleichung von lm_year_month liest sich also so:

Temperatur ist eine Funktion von der (zentrierten) Jahreszahl und des Monats

lm_year_month <- lm(precip ~ year_c + month_factor, 
                    data = wetter_month_1_7)

Die Modellparameter sind in Tabelle 10.8 zu sehen.

Tabelle 10.8: Modellparameter von lm_year_month

Fixed Effects

Coefficient	Parameter	CI
56.94	(Intercept)	(55.60, 58.27)
0.03	year_c	(5.59e-03, 0.05)
24.37	month_factor7	(22.48, 26.27)

Die Modellkoeffizienten sind so zu interpretieren:

1. Achsenabschnitt (${\beta }_0$, Intercept): Im Referenzjahr (1951) im Referenzmonat Januar lag die Niederschlagsmenge bei 57$$mm pro Quadratmeter.
2. Regressionskoeffizient für Jahr (${\beta }_1$, year_c): Pro Jahr ist die Niederschlagsmenge im Schnitt um 0.03$$mm an (im Referenzmonat).
3. Regressionskoeffizient für Monat (${\beta }_2$, month_factor7) Im Monat 7 (Juli) lag die mittlere Niederschlagsmenge (im Referenzjahr) knapp 25$$mm über dem mittleren Wert des Referenzmonats (Januar).

Die Regressiongleichung von lm_year_month lautet: precip_pred = 56.94 + 0.03*year_c + 24.37*month_factor_7. Im Monat Juli ist month_factor_7 = 1, ansonsten (Januar) ist month_factor = 0. Demnach erwarten wir laut Modell lm_year_month im Juli des Referenzjahres 81.31$$mm Niederschlag. Die Werte der Regressionskoeffizienten sind Tabelle 10.8 entnommen.

🧑‍🎓 Puh, kompliziert!

🧑‍🏫 Es gibt einen Trick, man kann sich von R einfach einen beliebigen Y-Wert berechnen lassen, s. Beispiel 10.12.

Beispiel 10.12 (Niederschlag laut Modell Im Juli 2020?) Hey R, berechne uns anhand neuer Daten den laut Modell zu erwartenden Niederschlag für Juli im Jahr 2020!

neue_daten <- tibble(year_c = 2020-1951,
                     month_factor = factor("7"))
predict(lm_year_month, newdata = neue_daten)
##  1 
## 83

Das Modell erwartet Niederschlag in Höhe von 83.3$$mm. Mit predict kann man sich Vorhersagen eines Modells ausgeben lassen. $◻$

Alle Regressionskoeffizienten beziehen sich auf die AV unter der Annahme, dass alle übrigen UV den Wert Null (bzw. Referenzwert) aufweisen.

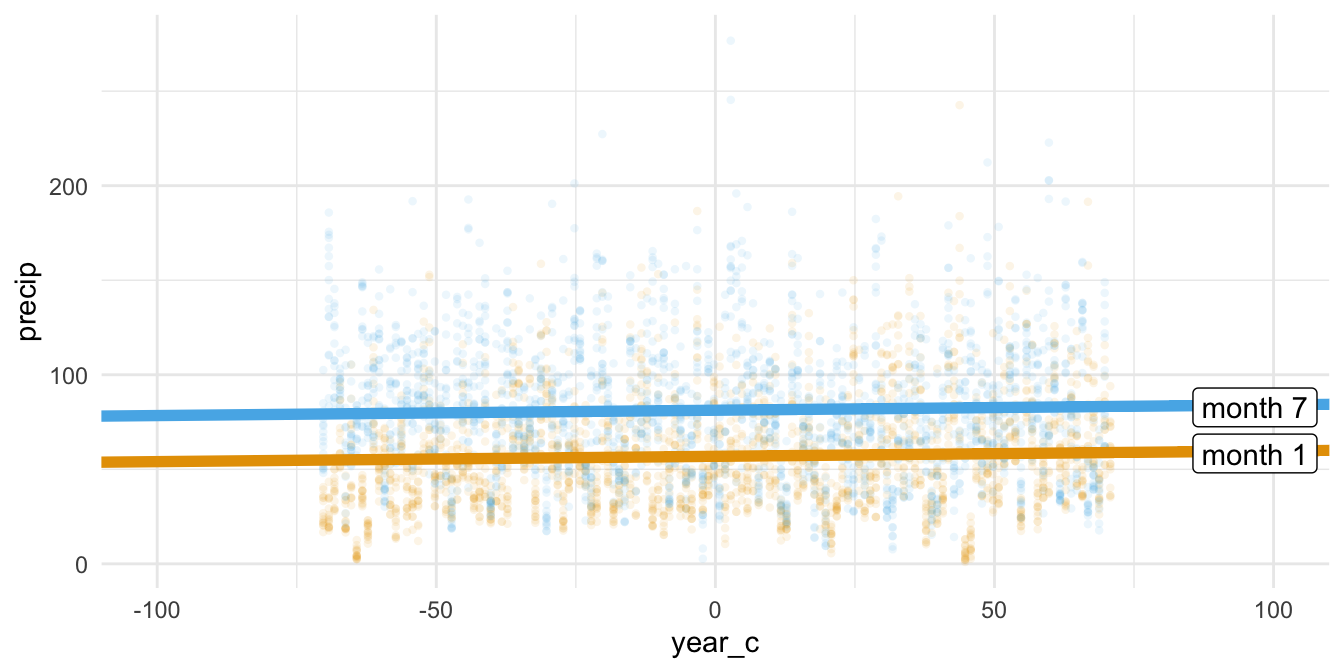
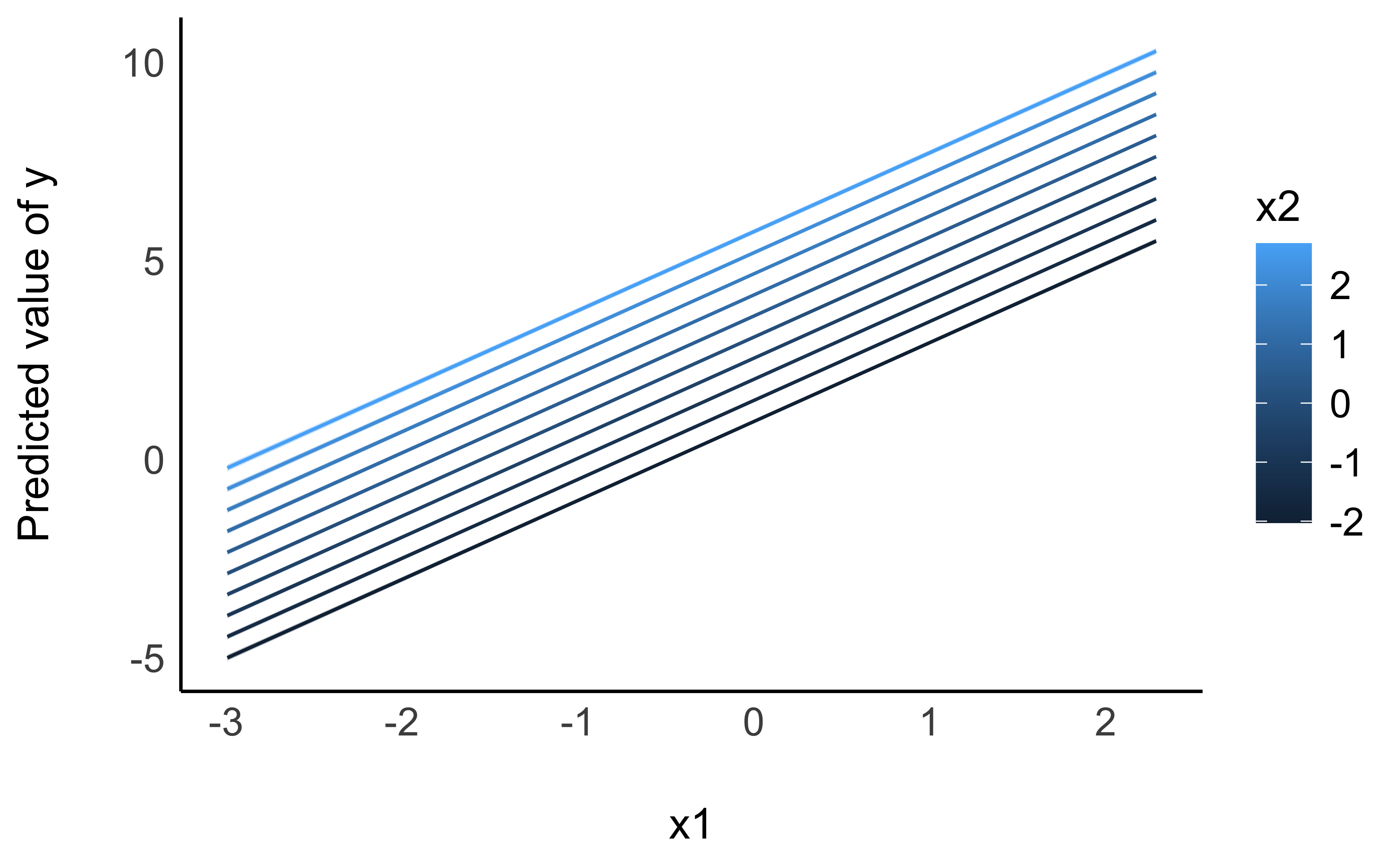
Visualisieren wir uns die geschätzten Erwartungswert pro Wert der UV, s. Abbildung 10.10: plot(estimate_expectation(lm_year_month))

Abbildung 10.10: Niederschlag für Januar (month 1) und Juli (month 7) im Verlauf der Jahre. Man beachte, dass die Regressionsgeraden parallel sind.

Mit scale_color_okabeito haben wir die Standard-Farbpalette durch die von Okabe & Ito (2023) ersetzt (s. Barrett, 2021). Das ist nicht unbedingt nötig, aber robuster bei Sehschwächen, vgl. Kapitel 5.10.3. Die erklärte Varianz von lm_year_month liegt bei:

r2(lm_year_month)
## # R2 for Linear Regression
##        R2: 0.124
##   adj. R2: 0.124

10.3.6 Interaktion

Eine Modellgleichung der Form temp ~ year + month zwingt die Regressionsgeraden dazu, parallel zu verlaufen. Aber vielleicht würden sie besser in die Punktewolken passen, wenn wir ihnen erlauben, auch nicht parallel verlaufen zu dürfen? Nicht-parallele Regressionsgeraden erlauben wir, indem wir das Regressionsmodell wie folgt spezifizieren und visualisieren, s. Listing 10.1.

Listing 10.1: Ein Interaktionsmodell spezifiziert man in dieser Art: y ~ x1 + x2 + x1:x2

lm_year_month_interaktion <- lm(
  precip ~ year_c + month_factor + year_c:month_factor, 
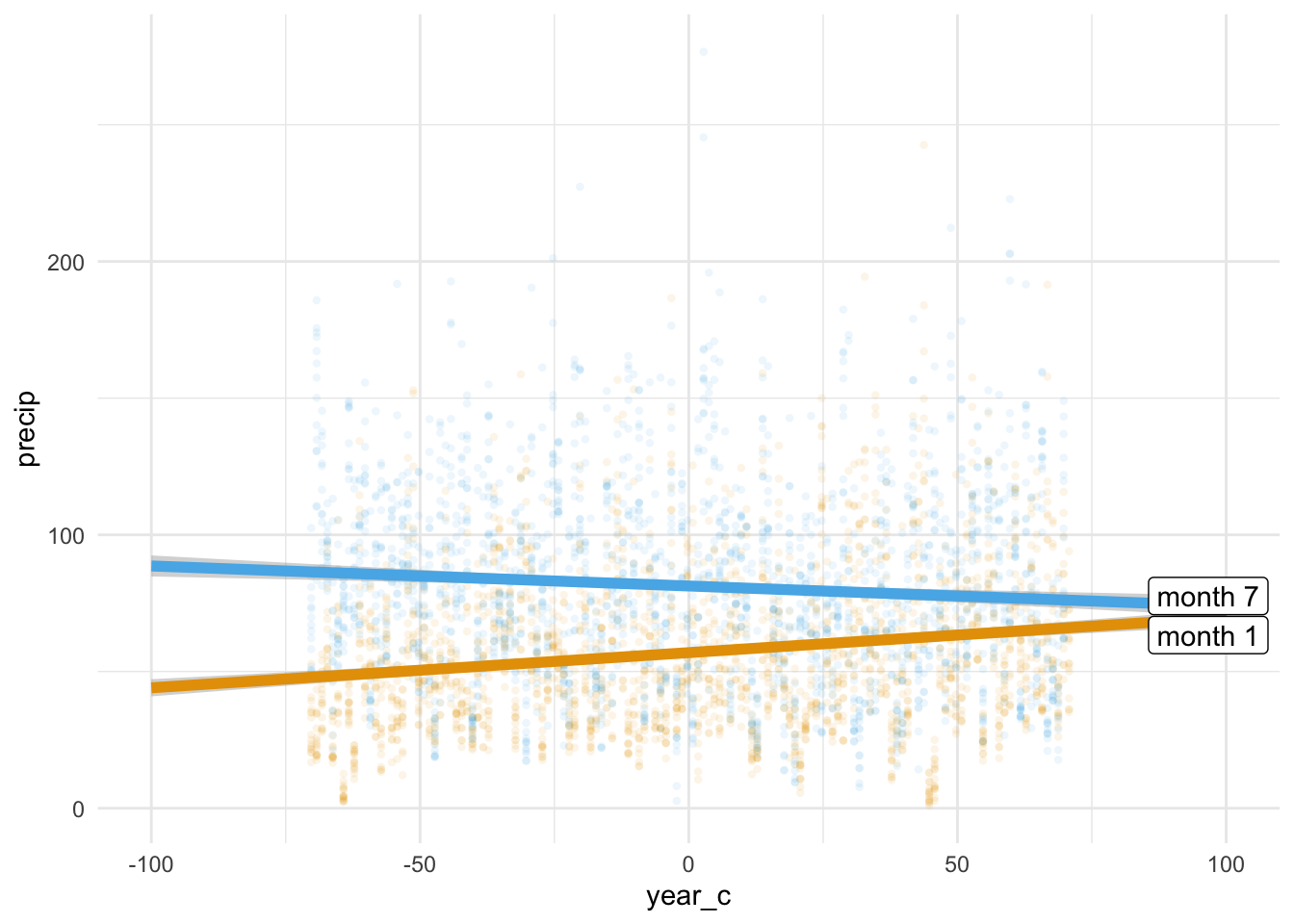
  data = wetter_month_1_7)

Visualisiert ist das Modell in Abbildung 10.11.

plot(estimate_relation(lm_year_month_interaktion)) 

Abbildung 10.11: Niederschlag im Jahresverlauf und Monatsvergleich mit Interaktionseffekt: Die Veränderung im Verlauf der Jahre ist unterschiedlich für die Monate (Januar vs. Juli). Die beiden Regressionsgeraden sind nicht parallel.

Der Doppelpunkt-Operator (:) fügt der Regressionsgleichung einen Interaktionseffekt hinzu, in diesem Fall die Interaktion von Jahr (year_c) und Monat (month_factor):

precip ~ year_c + month_factor + year_c:month_factor

Definition 10.4 (Interaktionseffekt) Einen Interaktionseffekt von x1 und x2 kennzeichnet man in R mit dem Doppelpunkt-Operator, x1:x2:

y ~ x1 + x2 + x1:x2 $◻$

In Worten:

y wird modelliert als eine Funktion von x1 und x2 und dem Interaktionseffekt von x1 mit x2.

Wie man in Abbildung 10.11 sieht, sind die beiden Regressionsgeraden nicht parallel. Sind die Regressionsgeraden von zwei (oder mehr) Gruppen nicht parallel, so liegt ein Interaktionseffekt vor. In diesem Fall ist der Interaktionsffekt ungleich Null. $◻$

Beispiel 10.13 (Interaktionseffekt von Niederschlag und Monat) Wie ist die Veränderung der Niederschlagsmenge (Y-Achse) im Verlauf der Jahre (X-Achse)? Das kommt darauf an, welchen Monat man betrachtet. Der Effekt der Zeit ist unterschiedlich für die Monate: Im Juli nahm der Niederschlag ab, im Januar zu. $◻$

Liegt ein Interaktionseffekt vor, kann man nicht mehr von “dem” (statistischen) Effekt einer UV (auf die AV) sprechen. Vielmehr muss man unterscheiden: Je nach Gruppe (z.$$B. Monat) unterscheidet der Effekt des Jahres auf die Niederschlagsmenge. (“Effekt” ist hier immer statistisch, nie kausal gemeint.) Betrachten wir die Parameterwerte des Interaktionsmodells, s. Tabelle 10.9.

Tabelle 10.9: Modellparameter von lm_year_month_interaktion

Parameter	Coefficient	CI_low	CI_high
(Intercept)	56.91	55.59	58.24
year_c	0.13	0.10	0.16
month_factor7	24.37	22.50	26.25
year_c:month_factor7	-0.20	-0.25	-0.16

Neu bei der Ausgabe zu diesem Modell ist die unterste Zeile für den Parameter year c × month factor [7]. Sie gibt die Stärke des Interaktionseffekts an. Die Zeile zeigt, wie unterschiedlich sich die die Niederschlagsmenge zwischen den beiden Monaten im Verlauf der Jahre ändert: Pro Jahr ist die Zunahme an Niederschlag um 0.20$$mm geringer als im Referenzmonat (Januar). Damit resultiert für Juli insgesamt ein positiver Effekt: 0.13 - -0.20 = 0.07. Insgesamt lautet die Regressionsgleichung: precip_pred = 56.91 + 0.13 * year_c + 24.37 * month_factor_7 - 0.20 * year_c:month_factor_7.

Wichtig

Der Achsenabschnitt gibt den Wert der AV an unter der Annahme, dass alle UV den Wert Null aufweisen. $◻$

Wenn eine Beobachtung in allen UV den Wert 0 hat, so gibt der Achsenabschnitt den Niederschlag für den Januar des Jahres 1951 an. Die Regressionskoeffizienten geben die Zunahme in der AV an, wenn der jeweilige Wert der UV um 1 steigt, die übrigen UV aber den Wert 0 aufweisen.

Das $R^2$ von lm_year_month_interaktion beträgt übrigens nur geringfügig mehr als im Modell ohne Interaktion:

r2(lm_year_month_interaktion)  # aus `{easystats}`
## # R2 for Linear Regression
##        R2: 0.139
##   adj. R2: 0.138

Da man Modelle so einfach wie möglich halten sollte, könnten wir auf den Interaktionseffekt im Modell verzichten. Der Interaktionseffekt verbessert die Modellgüte nur geringfügig. Falls wir aber von einer starken Theorie ausgehen, die den Interaktionseffekt verlangt, hätten wir einen triftigen Grund, den Interaktionseffekt im Modell zu belassen.

10.4 Modelle mit vielen UV

10.4.1 Zwei metrische UV

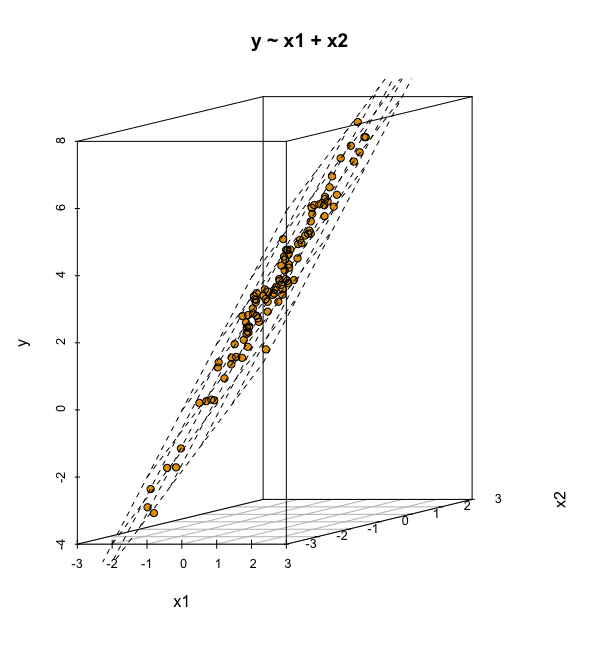
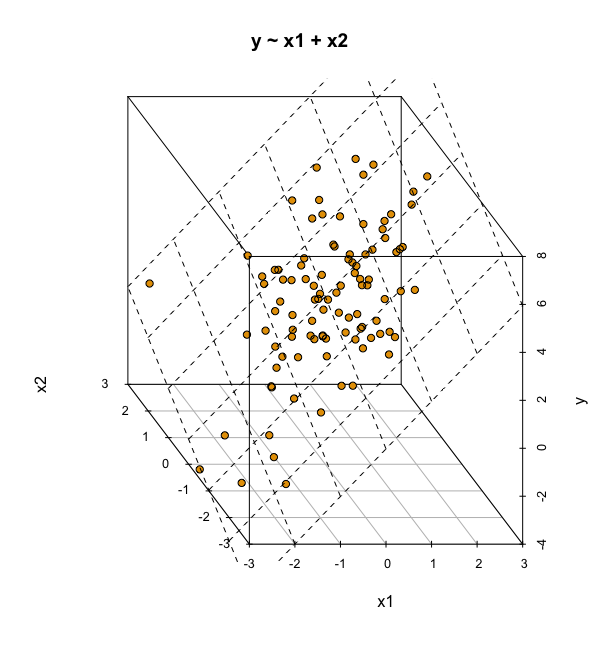
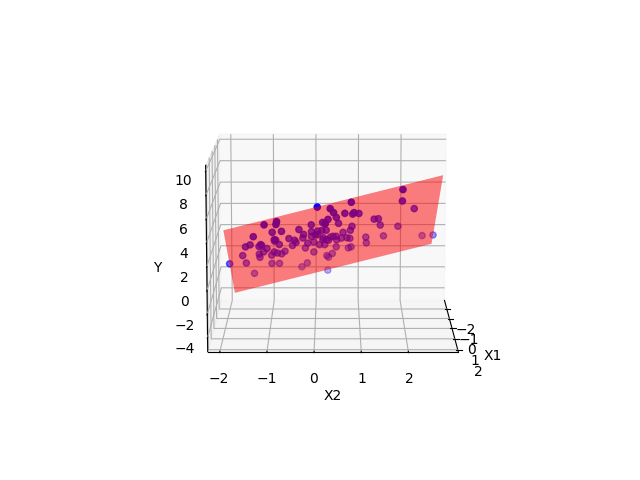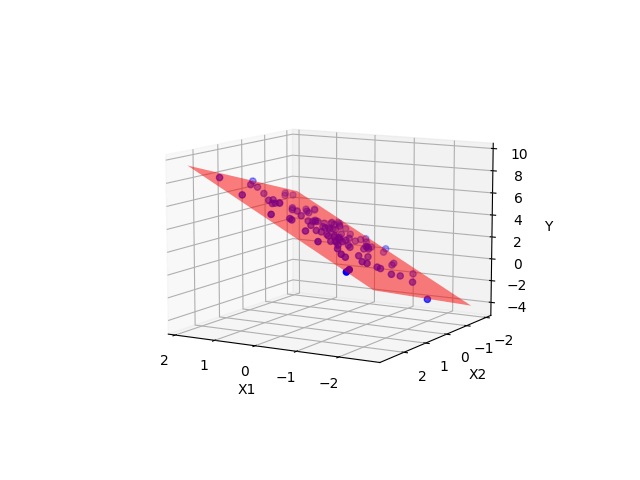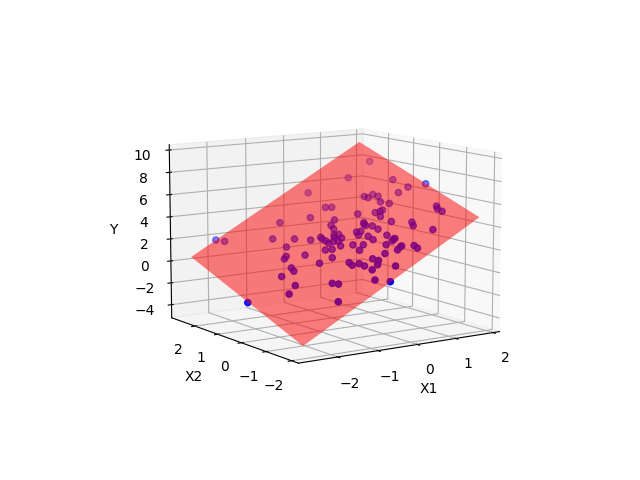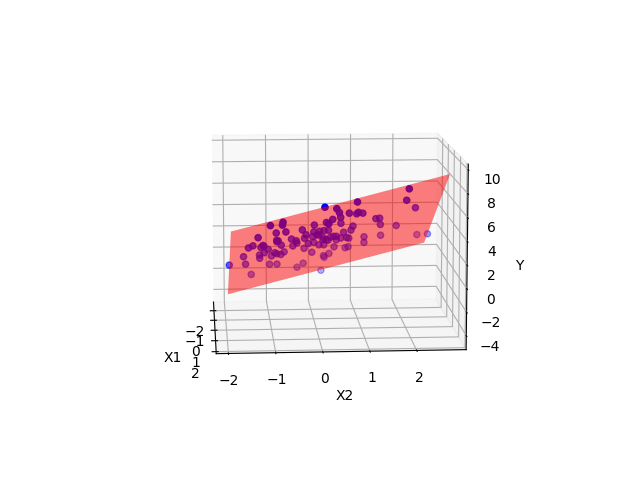
Ein Modell mit zwei metrischen UV kann man sich im 3D-Raum visualisieren, s. Abbildung 10.12, oder im 2D-Raum, s. Abbildung 10.13. Im 3D-Raum wird die Regressionsgerade zu einer Regressionsebene.

Winkel 1

Winkel 2

Winkel 3

Abbildung 10.12: Ein lineares Modell, y ~ x1 + x2 mit zwei UV im 3D-Raum.

Abbildung 10.13: 2D-Diagramm für 3D-Modell

3D-Animation

(a) Animation eines Regeressionsmodells mit zwei metrischen UV, x1 und x2; y wird gut von den beiden UV erklärt

2D-Diagramm für 3D-Modell

Abbildung 10.14

Grundsätzlich kann man viele UV in ein (lineares) Modell aufnehmen. Betrachten wir z.$$B. folgendes lineares Modell mit zwei metrischen UV, lm_mario_2uv.

lm_mario_2uv <- lm(total_pr ~ start_pr + ship_pr, 
                   data = mariokart %>% filter(total_pr < 100))

10.4.2 Viele UV ins Modell?

Wir könnten im Prinzip alle Variablen unserer Datentabelle als UV in das Regressionsmodell aufnehmen. Die Frage ist nur: Macht das Sinn? Hier sind einige Richtlinien, die helfen, welche Variablen (und wie viele) man als UV in ein Modell aufnehmen sollte [Gelman et al. (2021);. S. 199], wenn das Ziel eine möglichst hohe Modellgüte ist:

1. Man sollte alle Variablen aufnehmen, von denen anzunehmen ist, dass Sie Ursachen für die Zielvariablen sind.
2. Bei UV mit starken (absoluten) Effekten kann es Sinn machen, ihre Interaktionseffekte auch mit in das Modell aufzunehmen.
3. UV, die vergleichsweise exakt geschätzt werden (der Bereich 95 CI ist klein), sollten tendenziell im Modell belassen werden, da sie die Modellgüte verbessern.

Ist das Ziel hingegen, eine Theorie bzw. ein wissenschaftliches Modell zu überprüfen, so sollte man genau die UV in das Modell aufnehmen, die die Theorie verlangt.

10.5 Fallbeispiel zur Prognose

Beispiel 10.14 (Prognose des Verkaufspreis) Ganz können Sie von Business-Welt und ihren Gratifikationen nicht lassen, trotz Ihrer wissenschaftlichen Ambitionen. Sie haben den Auftrag bekommen, den Verkaufspreis von Mariokart-Spielen möglichst exakt vorherzusagen. Also gut, das Honorar ist phantastisch, Sie sind jung und brauchen das Geld. $◻$

10.5.1 Modell “all-in”

Um die Güte Ihrer Vorhersagen zu prüfen, teilt Ihre Chefin den Datensatz in zwei zufällige Teile.

👩‍💼 Ich teile den Datensatz mariokart zufällig in zwei Teile. Den ersten Teil kannst du nutzehn, um Modelle zu berechnen (“trainieren”) und ihre Güte zu prüfen. Den Teil nenne ich “Train-Sample”, hört sich cool an, oder? Im Train-Sample ist ein Anteil (fraction) von 70% der Daten, okay? Die restlichen Daten behalte ich. Wenn du ein gutes Modell hast, kommst du und wir berechnen die Güte deiner Vorhersagen in dem verbleibenden Teil, die übrigen 30% der Daten. Diesen Teil nennen wir Test-Sample, alles klar?

Wenn die Daten in Ihrem Computer zu finden sind, z.$$B. im Unterordner data, dann können Sie sie von dort importieren:

mariokart_train <- read.csv("data/mariokart_train.csv")

Alternativ können Sie sie auch von diesem Pfad von einem Rechner in der Cloud herunterladen:

mariokart_train <- read.csv("https://raw.githubusercontent.com/sebastiansauer/statistik1/main/data/mariokart_train.csv")

Dann importieren wir auf gleiche Weise Test-Sample in R:

mariokart_test <- read.csv("https://raw.githubusercontent.com/sebastiansauer/statistik1/main/data/mariokart_test.csv")

Also los. Sie probieren mal die “All-in-Strategie”: Alle Variablen rein in das Modell. Viel hilft viel, oder nicht?

lm_allin <- lm(total_pr ~ ., data = mariokart_train)
r2(lm_allin)  # aus easystats
## # R2 for Linear Regression
##        R2: 0.994
##   adj. R2: 0.980

Der Punkt in total_pr ~ . heißt “alle Variablen in der Tabelle (außer total_pr)”.

👩‍💼 Hey! Das ist ja fast perfekte Modellgüte!

🦹‍♀️️ Vorsicht: Wenn ein Angebot aussieht wie “too good to be true”, dann ist es meist auch too good to be true.

Der Grund für den fast perfekten Modellfit ist die Spalte Title. Unser Modell hat einfach den Titel jeder Auktion auswendig gelernt. Weiß man, welcher Titel zu welcher Auktion gehört, kann man perfekt die Auktion aufsagen bzw. das Verkaufsgebot perfekt vorhersagen. Leider nützen die Titel der Auktionen im Train-Sample nichts für andere Auktionen. Im Test-Sample werden unsere Vorhersagen also grottenschlecht sein, wenn wir uns auf die Titel der Auktionen im Test-Sample stützen. Merke: Höchst idiografische Informationen wie Namen, Titel etc. sind nicht nützlich, um allgemeine Muster zu erkennen und damit exakte Prognosen zu erstellen.

Probieren wir also die Vorhersage im Test-Sample:

predict(lm_allin, newdata = mariokart_test)
## Error in model.frame.default(Terms, newdata, na.action = na.action, xlev = object$xlevels): factor title has new levels MARIO KART FOR NINTENDO Wii WITH 2 WHEELS + GAME, Mario Kart Wii (Wii) COMPLETE , Mario Kart Wii (Wii) game , Mario Kart Wii (Wii) game and 2 wheels!, Mario Kart Wii (Wii) Game and Steering Wheel, Mario Kart Wii (Wii) Includes Steering Wheel!, MarioKart (Wii) w/ wheel

Oh nein! Was ist los!? Eine Fehlermeldung!

Nominalskalierte UV mit vielen Ausprägungen, wie title sind problematisch. Kommt eine Ausprägung von title im Test-Sample vor, die es nicht im Train-Sample gab, so resultiert ein Fehler beim predicten. Häufig ist es ohnehin sinnvoll, auf diese Variable zu verzichten, da diese Variablen oft zu Overfitting führen.

10.5.2 Modell “all-in”, ohne Titelspalte

Okay, also auf die Titelspalte sollten wir vielleicht besser verzichten. Nächster Versuch.

mariokart_train2 <-
  mariokart_train %>% 
  select(-c(title, id))

lm_allin_no_title_no_id <- lm(total_pr ~ ., data = mariokart_train2)
r2(lm_allin_no_title_no_id) 
## # R2 for Linear Regression
##        R2: 0.521
##   adj. R2: 0.441

Das R-Quadrat ist durchaus ordentlich.

🤖 Das haben wir gut gemacht!

performance::rmse(lm_allin_no_title_no_id)
## [1] 20

Sie rennen zu Ihrer Chefin, die jetzt die Güte Ihrer Vorhersagen in den restlichen Daten bestimmen soll.

👩‍💼 Da wir dein Modell in diesem Teil des Komplett-Datensatzes testen, nennen wir diesen Teil das “Test-Sample”.

Ihre Chefin schaut sich die Verkaufspreise im Test-Sample an:

mariokart_test %>% 
  select(id, total_pr) %>% 
  head()

id	total_pr
1.2e+11	37
2.9e+11	55
1.8e+11	56
1.8e+11	56
3.5e+11	65
1.1e+11	46

👩‍💼️ Okay, hier sind die ersten paar echten Verkaufspreise. Jetzt mach mal deine Vorhersagen auf Basis deines besten Modells!

Berechnen wir die Vorhersagen (engl. predictions; to predict: vorhersagen):

lm_allin_predictions <- predict(lm_allin_no_title_no_id, newdata = mariokart_test)

Hier sind die ersten paar Vorhersagen:

head(lm_allin_predictions)
##  1  2  3  4  5  6 
## 29 54 53 54 42 47

Diese Vorhersagen fügen wir noch der Ordnung halber in die Tabelle mit den Test-Daten ein:

mariokart_test <-
  mariokart_test %>% 
  mutate(lm_allin_predictions = predict(lm_allin_no_title_no_id, 
newdata = mariokart_test))

👩‍💼️ Okay, was ist jetzt der mittlere Vorhersagefehler?

Um die Vorhersagegüte im Test-Sample auszurechnen (wir verwenden dazu die Funktionen mae und rsq, nutzen wir die Funktionen des R-Paketes yardstick (welches Sie vielleicht noch installieren müssen):

library(yardstick)

yardstick::mae(data = mariokart_test,
               truth = total_pr,  # echter Verkaufspreis
               estimate = lm_allin_predictions)  # Ihre Vorhersage
yardstick::rmse(data = mariokart_test,
               truth = total_pr,  # echter Verkaufspreis
               estimate = lm_allin_predictions)  # Ihre Vorhersage

.metric	.estimator	.estimate
mae	standard	10

.metric	.estimator	.estimate
rmse	standard	13

Ihr mittlerer Vorhersagefehler (RMSE) liegt bei ca. 13 Euro. Übrigens haben wir hier yardstick::rmse geschrieben und nicht nur rmse, da es sowohl im Paket performance ( Teil des Metapakets easystats) als auch im Paket yardstick (Teil des Metapakets tidymodels) einen Befehl des Namens rmse gibt. Name-Clash-Alarm! R könnte daher den anderen rmse meinen als Sie, was garantiert zu Verwirrung führt. (Entweder bei R oder bei Ihnen.)

👩‍💼 Ganz okay.

Wie ist es um das R-Quadrat Ihrer Vorhersagen bestellt?

# `rsq ` ist auch aus dem Paket yardstick:
rsq(data = mariokart_test,
    truth = total_pr,  # echter Verkaufspreis
    estimate = lm_allin_predictions)  # Ihre Vorhersage

.metric	.estimator	.estimate
rsq	standard	0.17

👴️ 17%, nicht berauschend, aber immerhin!

Wie das Beispiel zeigt, ist die Modellgüte im Test-Sample (leider) oft geringer als im Train-Sample. Die Modellgüte im Train-Sample ist mitunter übermäßig optimistisch. Dieses Phänomen bezeichnet man als Overfitting (Gelman et al., 2021). Bevor man Vorhersagen eines Modells bei der Chefin einreicht, bietet es sich, die Modellgüte in einem neuen Datensatz, also einem Test-Sample, zu überprüfen.

Wir haben hier die Funktion rsq aus dem Paket yardstick verwendet, da r2 nur die Modellgüte im Train-Sample ausrechnen kann. rsq kann die Modellgüte für beliebige Vorhersagewerte berechen, also sowohl aus dem Train- oder dem Test-Sample.

10.6 Vertiefung: Das Aufteilen Ihrer Daten

10.6.1 Analyse- und Assessment-Sample

Wenn Sie eine robuste Schätzung der Güte Ihres Modells erhalten möchten, bietet sich folgendes Vorgehen an (vgl. Abbildung 10.15):

1. Teilen Sie Ihren Datensatz (das Train-Sample) in zwei Teile: Das sog. Validation-Sample und das sog. Assessment-Sample.
2. Berechnen Sie Ihr Modell im ersten Teil Ihres Datensatzes (dem Validation-Sample).
3. Prüfen Sie die Modellgüte im zweiten Teil Ihres Datensatzes (dem Assessment-Sample)

Diese Aufteilung Ihres Datensatzatzes in diese zwei Teile nennt man auch Validierungsaufteilung (validation split); Sie können sie z.$$B. so bewerkstelligen:

library(rsample)  # ggf. noch installieren
mariokart <- read_csv("data/mariokart.csv")  # Wenn die CSV-Datei in einem Unterordner mit Namen "data" liegt

meine_aufteilung <- initial_split(mariokart, strata = total_pr)

initial_split wählt für jede Zeile (Beobachtung) zufällig aus, ob diese Zeile in das Analyse- oder in das Assessment-Sample kommen soll. Im Standard werden 75% der Daten in das Analyse- und 25% in das Assessment-Sample eingeteilt;⁷ das ist eine sinnvolle Aufteilung. Das Argument strata sorgt dafür, dass die Verteilung der AV in beiden Stichproben gleich ist. Es wäre nämlich blöd für Ihr Modell, wenn im Train-Sample z.$$B. nur die teuren, und im Test-Sample nur die günstigen Spiele landen würde. Anderes Beispiel: In den ersten Zeilen stehen nur Kunden aus Land A und in den unteren Zeilen nur aus Land B. In so einem Fall würde sich Ihr Modell unnötig schwer tun. Im nächsten Schritt können Sie anhand anhand der von initial_split bestimmten Aufteilung die Daten tatsächlich aufteilen. initial_split sagt nur, welche Zeile in welche der beiden Stichproben kommen soll. Die eigentliche Aufteilung wird aber noch nicht durchgeführt.

mariokart_train <- 
  training(meine_aufteilung)  # Analyse-Sample
mariokart_test <- 
  testing(meine_aufteilung)  # Assessment-Sample

training wählt die Zeilen aus, die in das Train-Sample ihres Train-Samples, d.h. Ihr Analyse-Sample, kommen sollen. testing wählt die Zeilen aus, die in das Test-Sample ihres Train-Samples, d.h. Ihr Assessment-Sample, kommen sollen.

Ich persönliche nenne die Tabelle mit den Daten gerne d_analysis bzw. d_assess, das ist kürzer zu tippen und einheitlich. Sie können aber auch ein eigenes Namens-Schema nutzen; was aber hilfreich ist, ist Konsistenz in der Benamung, außerdem Kürze und aussagekräftige Namen.

10.6.2 Train- vs. Test-Sample

Das Train-Sample stellt die bekannten Daten dar; aus denen können wir lernen, d.$$h. unser Modell berechnen. Das Test-Sample stellt das Problem der wirklichen Welt dar: Neue Beobachtungen, von denen man (noch) nicht weiß, was der Wert der AV ist. Der Zusammenhang dieser verschiedenen, aber zusammengehörigen Arten von Stichproben ist in Abbildung 10.15 dargestellt.

Definition 10.5 (Train-Sample) Den Datensatz, für die Sie sowohl UV als auch AV vorliegen haben, nennt man Train-Sample. $◻$

Definition 10.6 (Test-Sample) Den Datensatz, für den Sie nur Daten der UV, aber nicht zu der AV vorliegen haben, nennt man Test-Sample. $◻$

Abbildung 10.15: Verschiedene Arten von zusammengehörigen Stichprobenarten im Rahmen einer Prognosemodellierung

10.7 Praxisbezug

Ein Anwendungsbezug von moderner Datenanalyse ist es vorherzusagen, welche Kunden “abwanderungsgefährdet” sind, also vielleicht in Zukunft bald nicht mehr unsere Kunden sind (“customer churn”). Es gibt eine ganze Reihe von Untersuchungen dazu, z.$$B. die von Lalwani et al. (2022). Das Forschungsteam versuchen anhand von Daten und u.$$a. auch der linearen Regression vorherzusagen, welche Kunden abgewandert sein werden. Die Autoren berichten von einer Genauigkeit von über 80$$% im (besten) Vorhersagemodell.

10.8 Wie man mit Statistik lügt

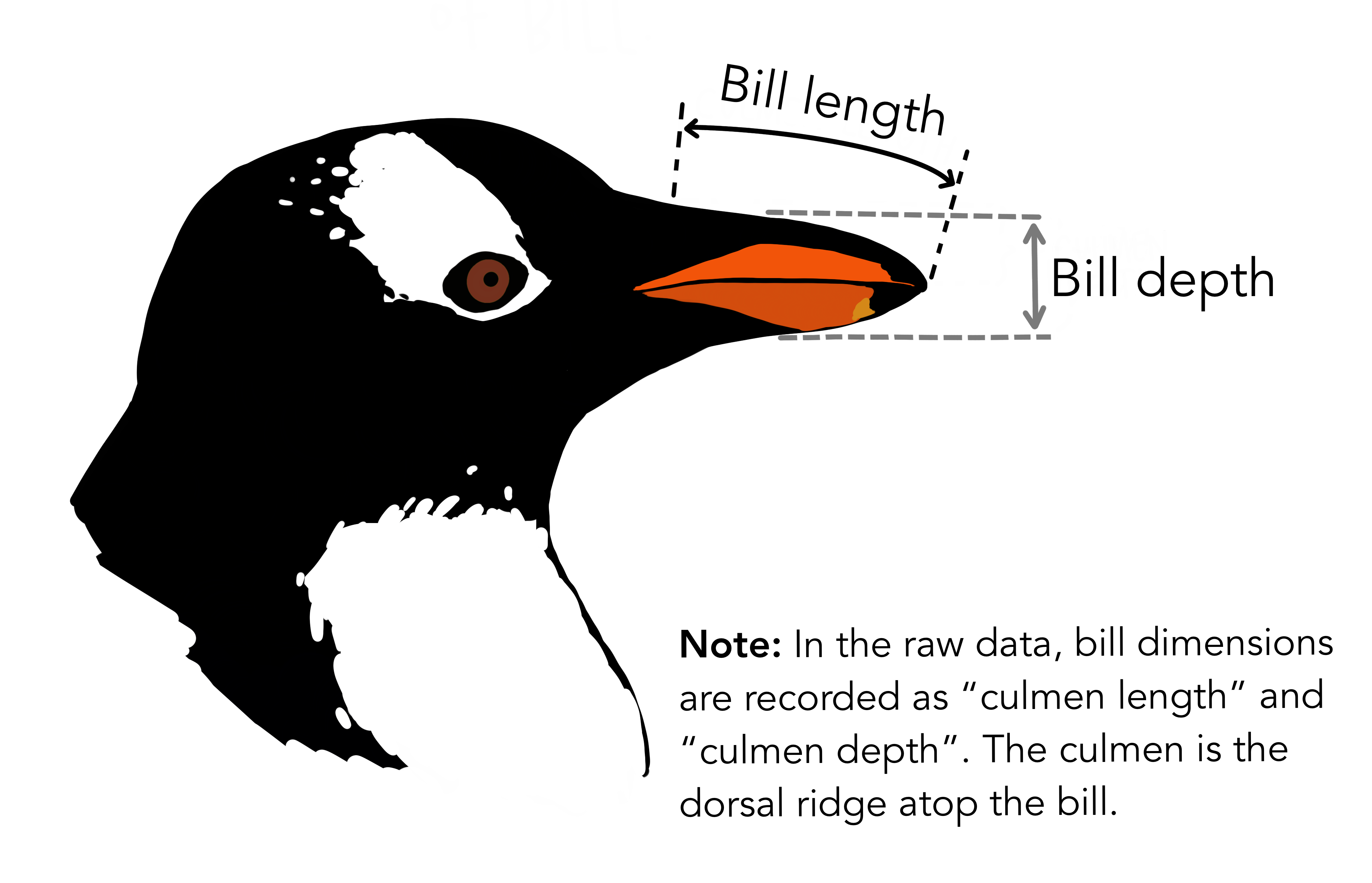
10.8.1 Pinguine drehen auf

Ein Forscher-Team untersucht Pinguine von der Palmer Station, Antarktis. Das Team ist am Zusammenhang von Schnabellänge (bill length) und Schnabeltiefe (bill depth) interessiert, s. Abbildung 10.16.

Abbildung 10.16: Schnabellänge und Schnabeltiefe; Horst (2024)

Das Team hat in schweißtreibender eiszapfentreibender Arbeit $n=344$ Tiere vermessen bei antarktischen Temperaturen. Hier sind die Daten:

penguins <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/palmerpenguins/penguins.csv")

10.8.2 Analyse 1: Gesamtdaten

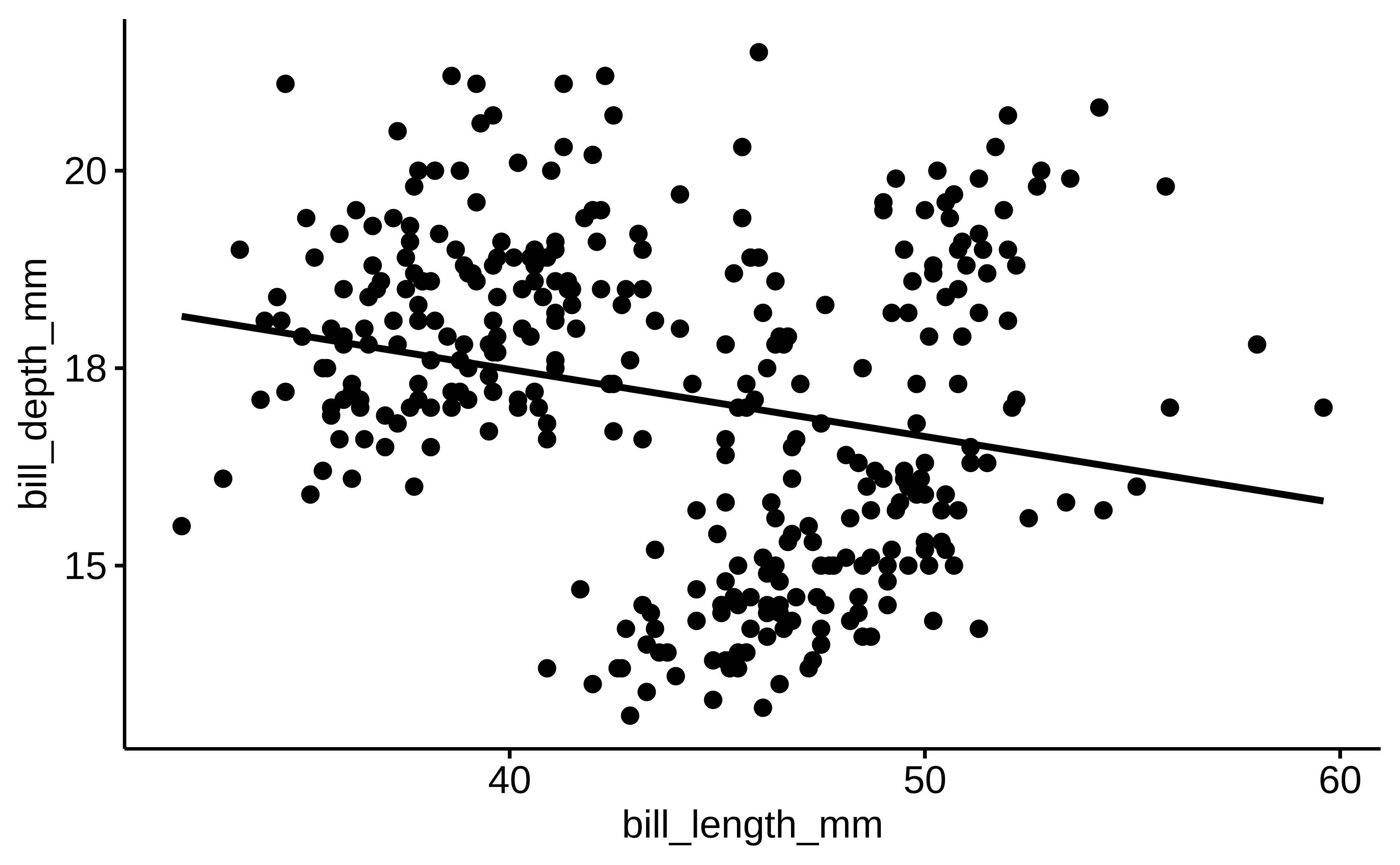
Man untersucht, rechnet und überlegt. Ah! Jetzt haben wir es! Klarer Fall: Ein negativer Zusammenhang von Schnabellänge und Schnabeltiefe, s. Abbildung 10.17. Das ist bestimmt einen Nobelpreis wert Schnell publizieren!

ggscatter(penguins, x = "bill_length_mm", y = "bill_depth_mm", 
          add = "reg.line")  # aus `ggpubr`

Abbildung 10.17: Negativer Zusammenhang von Schanbellänge und Schnabeltiefe

Hier sind die statistischen Details, s. Tabelle 10.10.

lm_ping1 <- lm(bill_depth_mm ~ bill_length_mm, data = penguins)

Tabelle 10.10: Koeffizienten des Modells 1: Negativer Effekt von bill_length_mm

Parameter	Coefficient
(Intercept)	20.89
bill_length_mm	-0.09

10.8.3 Analyse 2: Aufteilung in Arten (Gruppen)

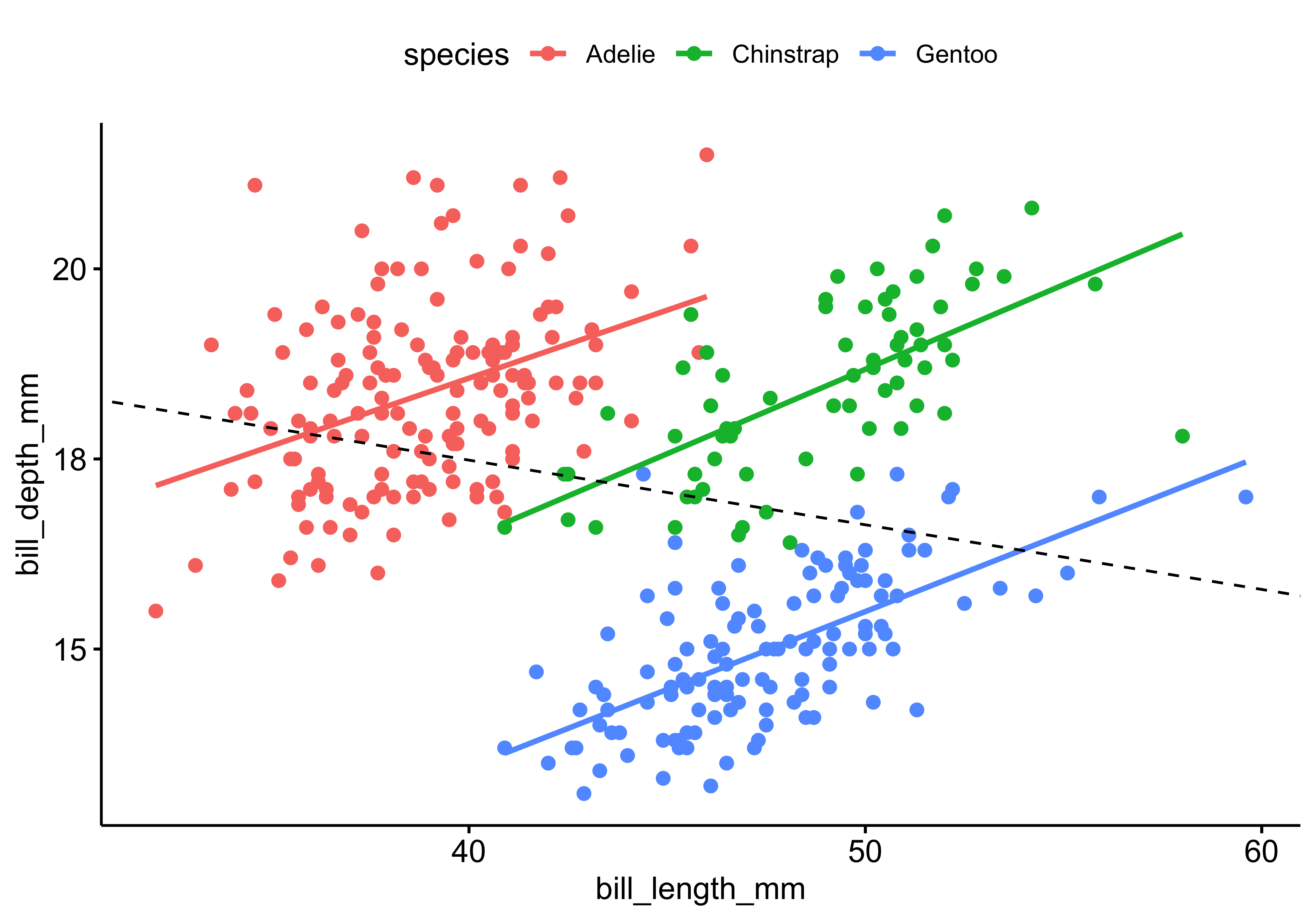
Kurz darauf veröffentlicht eine andere Forscherin auch einen Aufsatz zum gleichen Thema. Gleiche Daten. Aber mit gegenteiligem Ergebnis: Bei jeder Rasse von (untersuchten) Pinguinen gilt: Es gibt einen positiven Zusammenhang von Schnabelllänge und Schnabeltiefe, s. Abbildung 10.18.

Abbildung 10.18: Der Zusammenhang von Schnabelllänge und Schnabeltiefe pro Gruppe von Pinguinen: Die Regressionsgruppe pro Gruppe steigt. Hingegen sinkt die Regressionsgerade ohne Beachtung der Gruppen (schwarze gestrichelte Linie)

Oh nein! Was ist hier nur los? Daten lügen nicht?! Oder doch?!

Hier sind die statistischen Details der zweiten Analyse, s. Tabelle 10.11. Im zweiten Modell (lm2) kam species als zweite UV neu ins Modell (zusätzlich zur Schnabellänge).

lm_ping2 <- lm(bill_depth_mm ~ bill_length_mm + species, data = penguins)

Tabelle 10.11: Koeffizienten des Modells 2: Positiver Effekt von bill_length_mm

Parameter	Coefficient
(Intercept)	10.6
bill_length_mm	0.2
speciesChinstrap	-1.9
speciesGentoo	-5.1

Ohne Hintergrundwissen oder ohne weitere Analysen kann nicht entschieden werden, welche Analyse – Gesamtdaten oder Subgruppen – die richtige ist. Nicht-exprimentelle Studien können zu grundverschiedenen Ergebnissen führen, je nachdem, ob weitere UV dem Modell hinzugefügt oder weggenommen werden.

10.8.4 Vorsicht bei der Interpretation von Regressionskoeffizienten

Wichtig

Interpretiere Modellkoeffizienten nur kausal, wenn du ein Kausalmodell hast. $◻$

Nur wenn man die Ursache-Wirkungs-Beziehungen in einem System kennt, macht es Sinn, die Modellkoeffizienten kausal zu interpretieren. Andernfalls lässt man besser die Finger von der Interpretation der Modellkoeffizienten und begnügt sich mit der Beschreibung der Modellgüte und mit Vorhersage (synonym: Prognose). Wer das nicht glaubt, der betrachte Abbildung 10.19, links. Ein Forscher stellt das Modell m1: y ~ x auf und interpretiert dann b1: “Ist ja klar, X hat einen starken positiven Effekt auf Y!” In der nächsten Studie nimmt der Forscher dann eine zweite Variable, group (z.$$B. Geschlecht) in das Modell auf: m2: y ~ x + g. Oh Schreck! Jetzt ist b1 auf einmal nicht mehr stark positiv, sondern praktisch Null, und zwar in jeder Gruppe, s. Abbildung 10.19, rechts! Dieses Umschwenken der Regressionskoeffizienten kann nicht passieren, wenn der Effekt “echt”, also kausal, ist. Handelt es sich aber um “nicht echte”, also nicht-kausale Zusammenhänge, um Scheinzusammenhänge also, so können sich die Modellkoeffizienten dramatisch verändern, wenn man das Modell verändert, also Variablen hinzufügt oder aus dem Modell entfernt. Sogar das Vorzeichen des Effekts kann wechseln; das nennt man dann Simpsons Paradox (Gelman et al., 2021), Wenn man die kausalen Abhängigkeiten nicht kennt, weiß man also nicht, ob die Zusammenhänge kausal oder nicht-kausal sind. Dann bleibt unklar, ob die Modellkoeffizienten belastbar, robust, stichhaltig sind oder nicht.

(a) Modell: y ~ x, starker positiver Zusammenhang

 

(b) Modell: y ~ x + g, kein Zusammenhang in beiden Gruppe

Abbildung 10.19: Fügt man in ein Modell eine Variable hinzu, können sich die Koeffizienten massiv ändern. In beiden Diagrammen wurden die gleichen Daten verwendet. (a) starker positiver Zusammenhang, (b) kein Zusammenhang in beiden Gruppen

Man könnte höchstens sagen, dass man (wenn man die Kausalstruktur nicht kennt) die Modellkoeffizienten nur deskriptiv interpretiert, z.$$B. “Dort wo es viele Störche gibt, gibt es auch viele Babys” (Matthews, 2000).⁸ Leider ist unser Gehirn auf kausale Zusammenhänge geprägt: Es fällt uns schwer, Zusammenhänge nicht kausal zu interpretieren. Daher werden deskriptive Befunde immer wieder unzulässig kausal interpretiert – von Laien und Wissenschaftlern ebenfalls.

10.9 Was war noch mal das Erfolgsgeheimnis?

Wenn Sie dran bleiben an der Statistik, wird der Erfolg sich einstellen, s. Abbildung 10.20.

(a) Sie gestern

(b) Sie morgen

Abbildung 10.20: Statistik, Sie und Party: Gestern und (vielleicht) morgen. Wenn Sie dran bleiben, wird die Statistik Ihre beste Freundin (imgflip, 2024).

10.10 Fallstudien

Die folgenden Fallstudien zeigen auf recht anspruchsvollem Niveau (bezogen auf diesen Kurs) beispielhalft zwei ausführlichere Entwicklungen eines Prognosemodells.

Nutzen Sie diese Fallstudien, um sich intensiver mit der Entwicklung eines Prognosemodells auseinander zu setzen.

10.10.1 New Yorker Flugverspätungen 2023

Source

Vorhersage von Flugverspätungen

10.10.2 Filmerlöse

Vorhersagen von Filmerlösen

10.11 Vertiefung

Allison Horst erklärt die lineare Regression mit Hilfe von Drachen. 🐉 Sehenswert.

10.12 Aufgaben

Die Webseite datenwerk.netlify.app stellt eine Reihe von einschlägigen Übungsaufgaben bereit. Sie können die Suchfunktion der Webseite nutzen, um die Aufgaben mit den folgenden Namen zu suchen:

• interpret-koeff-lm
• Aussagen-einfache-Regr
• interpret-koeff
• regression1b
• mtcars-regr01
• regression1a
• lm1
• Regression5
• Regression6
• lm-mario1
• lm-mario2
• lm-mario3
• ausreisser1
• mario-compare-models

10.13 Literaturhinweise

Ein empfehlenswertes Buch für Regressionsanalyse ist das Buch von Andrew Gelman zum Thema “Regression und andere Geschichten” (Gelman et al., 2021). Sein Buch ist für Sozialwissenschaftler geschrieben, also nicht für typische Nerds, hat aber deutlich mehr Anspruch als dieses Kapitel. Eine Alternative bietet Sauer (2019).

Barrett, M. (2021). Ggokabeito: ’Okabe-Ito’ Scales for ’Ggplot2’ and ’Ggraph’ [Manual]. https://CRAN.R-project.org/package=ggokabeito

Deutscher Wetterdienst. (2025a). Regional averages DE, monthly air temperature mean. https://opendata.dwd.de/climate_environment/CDC/regional_averages_DE/monthly/air_temperature_mean/.

Deutscher Wetterdienst. (2025b). Regional averages DE, monthly precipitation mean. https://opendata.dwd.de/climate_environment/CDC/regional_averages_DE/monthly/precipitation/.

Gelman, A., Hill, J., & Vehtari, A. (2021). Regression and Other Stories. Cambridge University Press.

Habitator terrae. (2021). Deutsch: Fünfjährig Gemittelte Abweichung Der Lufftemperatur in Deutschland Vom Langjährigem Mittel 1951 Bis 1980 [Diagramm]. https://commons.wikimedia.org/wiki/File:%C3%84nderung_der_Lufttemperatur_in_Deutschland.gif

Horst, A. (2024). Statistics Artwork [Artwork]. https://allisonhorst.com/

imgflip. (2024). Imageflip Meme [Artwork]. https://imgflip.com

Kassambara, A. (2023). ggpubr: ’ggplot2’ Based Publication Ready Plots. https://CRAN.R-project.org/package=ggpubr

Kosinski, M., Stillwell, D., & Graepel, T. (2013). Private Traits and Attributes Are Predictable from Digital Records of Human Behavior. Proceedings of the National Academy of Sciences, 110(15), 5802–5805. https://doi.org/10.1073/pnas.1218772110

Kuhn, M., Vaughan, D., & Hvitfeldt, E. (2024). yardstick: Tidy Characterizations of Model Performance. https://CRAN.R-project.org/package=yardstick

Lalwani, P., Mishra, M. K., Chadha, J. S., & Sethi, P. (2022). Customer Churn Prediction System: A Machine Learning Approach. Computing, 104(2), 271–294. https://doi.org/10.1007/s00607-021-00908-y

Lüdecke, D., Ben-Shachar, M. S., Patil, I., Wiernik, B. M., Bacher, E., Thériault, R., & Makowski, D. (2022). easystats: Framework for Easy Statistical Modeling, Visualization, and Reporting. CRAN. https://doi.org/10.32614/CRAN.package.easystats

Matthews, R. (2000). Storks Deliver Babies (P= 0.008). Teaching Statistics, 22(2), 36–38. https://doi.org/10.1111/1467-9639.00013

Okabe, M., & Ito, K. (2023). Color Universal Design (CUD) / Colorblind Barrier Free. https://jfly.uni-koeln.de/color/

Sauer, S. (2019). Moderne Datenanalyse mit R: Daten einlesen, aufbereiten, visualisieren und modellieren. Springer. https://www.springer.com/de/book/9783658215866

Wickham, H., Averick, M., Bryan, J., Chang, W., McGowan, L. D., François, R., Grolemund, G., Hayes, A., Henry, L., Hester, J., Kuhn, M., Pedersen, T. L., Miller, E., Bache, S. M., Müller, K., Ooms, J., Robinson, D., Seidel, D. P., Spinu, V., … Yutani, H. (2019). Welcome to the tidyverse. Journal of Open Source Software, 4(43), 1686. https://doi.org/10.21105/joss.01686

Wilke, S. (2013, Juni 26). Trends der Lufttemperatur [Bericht]. Umweltbundesamt; Umweltbundesamt. https://www.umweltbundesamt.de/daten/klima/trends-der-lufttemperatur

---

1. Quelle: https://de.wikipedia.org/wiki/Zeitreihe_der_Lufttemperatur_in_Deutschland#cite_ref-3

2. Quelle: https://opendata.dwd.de/climate_environment/CDC/grids_germany/monthly/air_temperature_mean/

3. Ich danke Karsten Lübke für diese Idee.

4. In Abbildung 10.9? wird nicht der Schätzbereich für die Regressionsgewichte dargestellt, sondern stattdessen die SD der AV.

5. Zum Dollar-Operator s. Kapitel 3.11.3

6. synonym: nominalskalierte Variable

7. vgl. help(initial_split)

8. Das Störche-Babys-Beispiel passt auch zu Abbildung 10.19.