7 Modellgüte
Statistik, Prognose, Modellierung, R, Datenanalyse, Regression
\[ \definecolor{ycol}{RGB}{230,159,0} \definecolor{modelcol}{RGB}{86,180,233} \definecolor{errorcol}{RGB}{0,158,115} \definecolor{beta0col}{RGB}{213,94,0} \definecolor{beta1col}{RGB}{0,114,178} \definecolor{xcol}{RGB}{204,121,167} \]
7.1 Einstieg
In diesem Kapitel benötigen Sie die üblichen R-Pakete (tidyverse, easystats) und Daten (mariokart), s. Kapitel 3.7.3 und Kapitel 3.4.
mariokart <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/openintro/mariokart.csv")7.1.1 Lernziele
- Sie kennen gängige Maße der Streuung einer Stichprobe und können diese definieren und anhand von Beispielen erläutern.
- Sie können gängige Maße der Streuung einer Stichprobe mit R berechnen.
- Sie können die Bedeutung von Streuung für die Güte eines Modells erläutern.
Übungsaufgabe 7.1 (Freiwillige vor!) Für diese kleine Live-Demonstration brauchen wir einige Freiwillige. Die Lehrkraft teilt die Freiwilligen in zwei Gruppen ein: Gruppe Gleich-Groß und Gruppe Verschieden-Groß. Erkennen Sie, dass die Unterschiedlichkeit der Größe in Gruppe Gleich-Groß gering ist, aber in Gruppe Verschieden-Groß hoch? \(\square\)
7.1.2 Die Schlankheitspille von Prof. Weiss-Ois
Prof. Weiss-Ois hat eine Erfindung gemacht, eine Schlankheitspille💊 (flaticon, 2024).
Würden Sie die Pille von Prof. I. Ch. Weiss-Ois nehmen? Auf jeden Fall? Wenn Sie 1000\(\,\)Euro bekommen? Nur, wenn man Ihnen Geld zahlt? Auf keinen Fall?
Wie sehr die Werte eines Modells streuen, ist eine wichtige Information: Bei Prof. Weiss-Ois’ Pille kann es sein, dass Sie 10\(\,\)kg zunehmen, wenn Sie die Pille einnehmen.
7.1.3 Wie man seine Kuh über den Fluss bringt
Treffen sich zwei Bauern, Fritz Furchenzieher und Karla Kartoffelsack. Fritz will mit seiner Kuh einen Fluss überqueren, nur kann die Kuh nicht schwimmen (ob Fritz es kann, ist nicht überliefert).
👨🌾 (Fritz): Sag mal, Karla, ist der Fluss tief?
👩🌾 (Karla): Nö, im Schnitt nur einen Meter.
Also führt Fritz seine Kuh durch den Fluss, leider kam die Kuh nicht am anderen Ufer an, da im Floß ersoffen, s. Abbildung 7.2.
👩🌾 (Karla): Übrigens: Lagemaße sagen nicht alles, Fritz.
👨🌾 (Fritz): Läuft die Kuh durch den Fluss, kann sie schwimmen oder ’s ist Schluss.
Die Streuung ihrer Daten zu kennen, ist eine wesentliche Information. \(\square\)
7.2 Woran erkennt man ein gutes Modell?
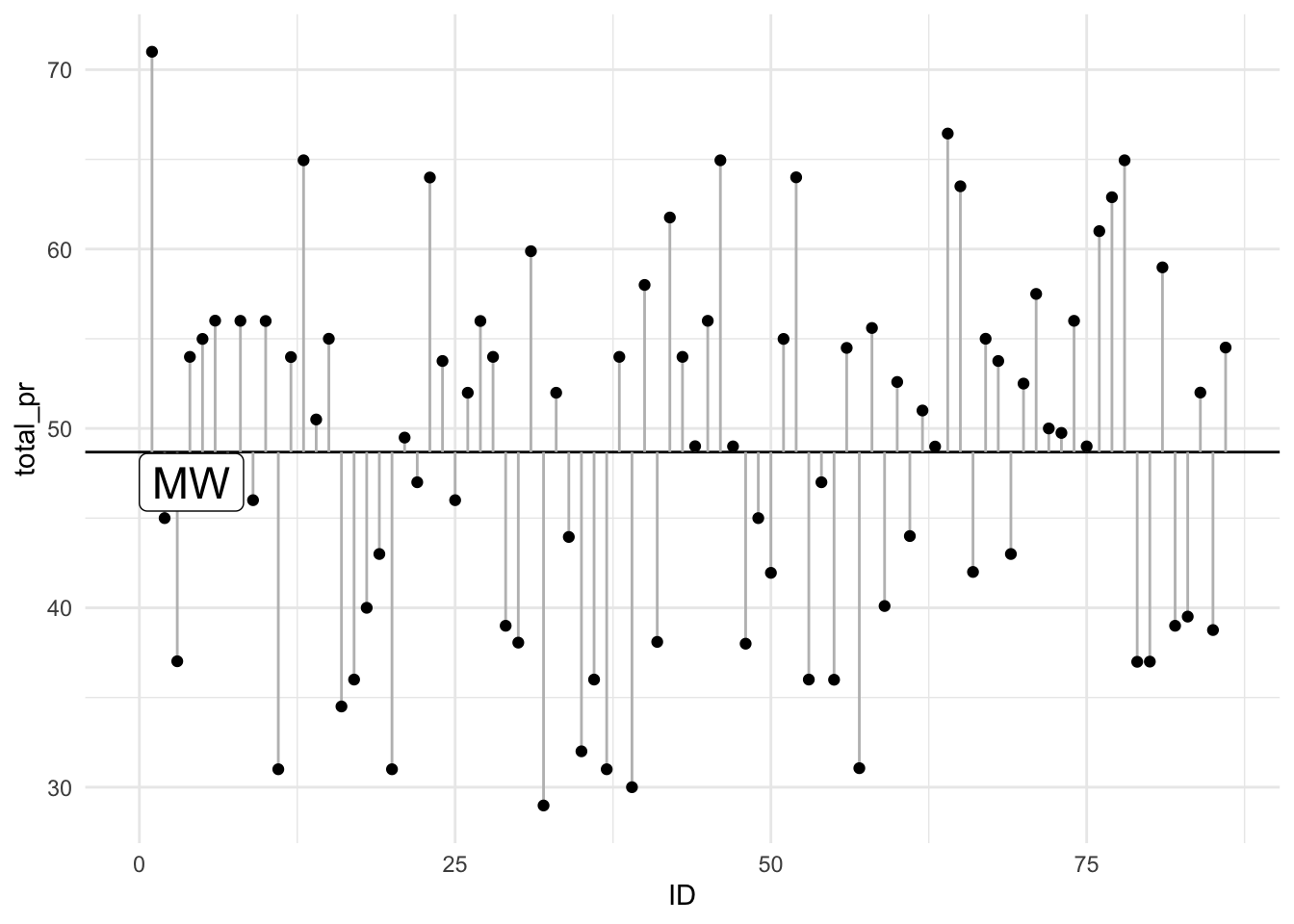
Abbildung 7.3 zeigt ein einfaches Modell (Mittelwert) mit wenig Streuung (links) vs. ein einfaches Modell mit viel Streuung (rechts). Links ist die Streuung der Schlankheitspille Dicktableitin und rechts von der Schlankheitspille Pfundafliptan abgetragen. Die vertikalen Balken in Abbildung 7.3 kennzeichnen den (absoluten) Abstand von jeweils einem Datenpunkt zum Mittelwert (horizontale Linie). Je länger die vertikalen ‘Abstandsbalken’ insgesamt, desto größer die Streuung. Die X-Achse (id) reiht die Versuchspersonen auf.
Bei einem Modell mit wenig Streuung liegen die tatsächlichen, beobachtete Werte (\(y\)) nah an den Modellwerten (vorhergesagten Werten, \(\hat{y}\)); die Abweichungen \(e = y - \hat{y}\) sind also gering (der Modellfehler ist klein). Bei einem Modell mit viel Streuung ist der Modellfehler \(e\) (im Vergleich dazu) groß.
Beispiel 7.1 (Daten zur Schlankheitskur von Prof. Weiss-Ois) In Abbildung 7.3 sind die Daten zu der Gewichtsveränderung nach Einnahme von “Schlankheitspillen” zweier verschiedener Präparate. Wie man sieht, unterscheidet sich die typische (vorhergesagte, mittlere) Gewichtsveränderung zwischen den beiden Präparaten kaum. Die Streuung allerdings schon. Links sieht man die Gewichtsveränderungen nach Einnahme des Präparats “Dickableibtin extra mild” und rechts das Präparat von Prof. Weiss-Ois’ “Pfundafliptan Forte”. Welches Präparat würden Sie lieber einnehmen?\(\square\)
Wir wollen ein präzises Modell, also kurze Fehlerbalken: Das Modell soll die Daten gut erklären, also wenig vom tatsächlichen Wert abweichen. Jedes Modell sollte Informationen über die Präzision des Modellwerts bzw. der Modellwerte (Vorhersagen) angeben. Ein Modell ohne Angaben der Modellgüte, d.\(\,\)h. der Präzision der Schätzung des Modellwerts, ist wenig nütze.
🧑🎓 Ich frage mich, ob man so ein Modell nicht verbessern kann?
🧑🏫 Die Frage ist, was wir mit “verbessern” meinen?
🧑🎓 Naja, kürzere Fehlerbalken, ist doch klar!
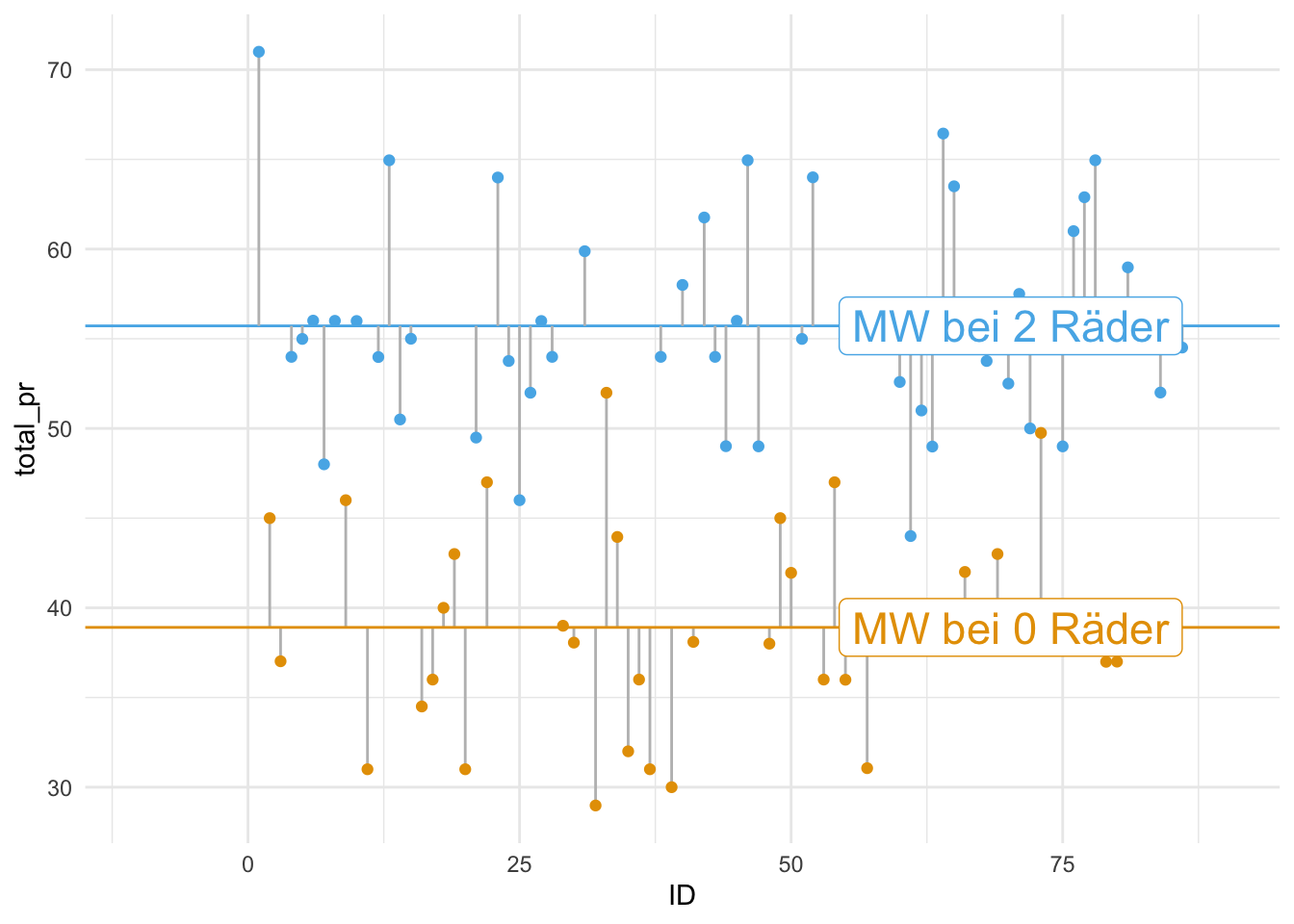
Im Beispiel von Mariokart: Da die Anzahl der Lenkräder mit dem Verkaufspreis zusammenhängt, könnte es vielleicht sein, dass wir die Lenkräder-Anzahl zur Vorhersage nutzen könnten. Das sollten wir ausprobieren. Abbildung 7.4 zeigt, dass die Fehlerbalken kürzer werden, wenn wir ein (sinnvolles) komplexeres Modell finden. Innerhalb jeder der beiden Gruppen (mit 2 Lenkrädern vs. mit 0 Lenkrädern) sind die Fehlerbalken jeweils im Durchschnitt kürzer (rechtes Teildiagramm) als im Modell ohne Gruppierung (linkes Teildiagramm). Aus Gründen der Übersichtlichkeit wurden nur Autos mit Verkaufsgebot von weniger als 100 Euros berücksichtigt und nur Spiele mit 0 oder mit 2 Lenkrädern.
Durch sinnvolle, komplexere Modelle sinkt die Fehlerstreuung eines Modells. \(\square\)
7.3 Streuungsmaße
Definition 7.1 (Streuungsmaße) Ein Streuungsmaß quantifiziert die Variabilität (Unterschiedlichkeit, Streuung) eines Merkmals. \(\square\)
Definition 7.2 (Spannweite) Ein einfaches Streuungsmaß ist die Spannweite (Range) \(R\), definiert als Differenz von größtem und kleinsten Wert eines Merkmals X: \(R := X_{max} - X_{min}. \square\)
Beispiel 7.2 Angenommen, wir haben einen Datensatz zum Merkmal “Alter” mit den Werte 1, 23, 42, 100. Dann beträgt der Range: \(R = 100 - 1 = 99\). Das bedeutet, dass die Werte des Merkmals sich über 99 Einheiten (Jahre in diesem Fall) verteilen. \(\square\)
Die Spannweite ist aber nicht robust (gegenüber Extremwerten) und sollte daher nur mit Einschränkung verwendet werden.
7.3.1 Der mittlere Abweichungsbalken
🧑🎓 Wir müssen jetzt mal präziser werden! Wie können wir die Streuung berechnen?
🧑🏫 Gute Frage! Am einfachsten ist es, wenn wir die mittlere Länge eines Abweichungsbalkens ausrechnen.
Legen wir (gedanklich) alle Abweichungsbalken \(e\) aneinander und teilen durch die Anzahl \(n\) der Balken, so erhalten wir den “mittleren Abweichungsbalken”, den wir mit \(\bar{e}\) (“e quer”) bezeichnen könnten. Diesen Kennwert bezeichnet man als Mean Absolute Error (MAE) bzw. als mittlere Absolutabweichung (MAA), s. Gleichung 7.1.
Definition 7.3 (Mittlere Absolutabweichung) Die Mittlere Absolutabweichung (MAA, MAE) ist definiert als die Summe der Absolutwerte der Differenzen eines Messwerts zum Mittelwert, geteilt durch die Anzahl der Messwerte. (Wenn man solche Sätze liest, fühlt sich die Formel fast einfacher an.)
\[{\displaystyle \mathrm {MAE} :={\frac {\sum _{i=1}^{n}\left|y_{i}-\bar{y}\right|}{n}}={\frac {\sum _{i=1}^{n}\left|e_{i}\right|}{n}}=\bar{e}. \; \square} \tag{7.1}\]
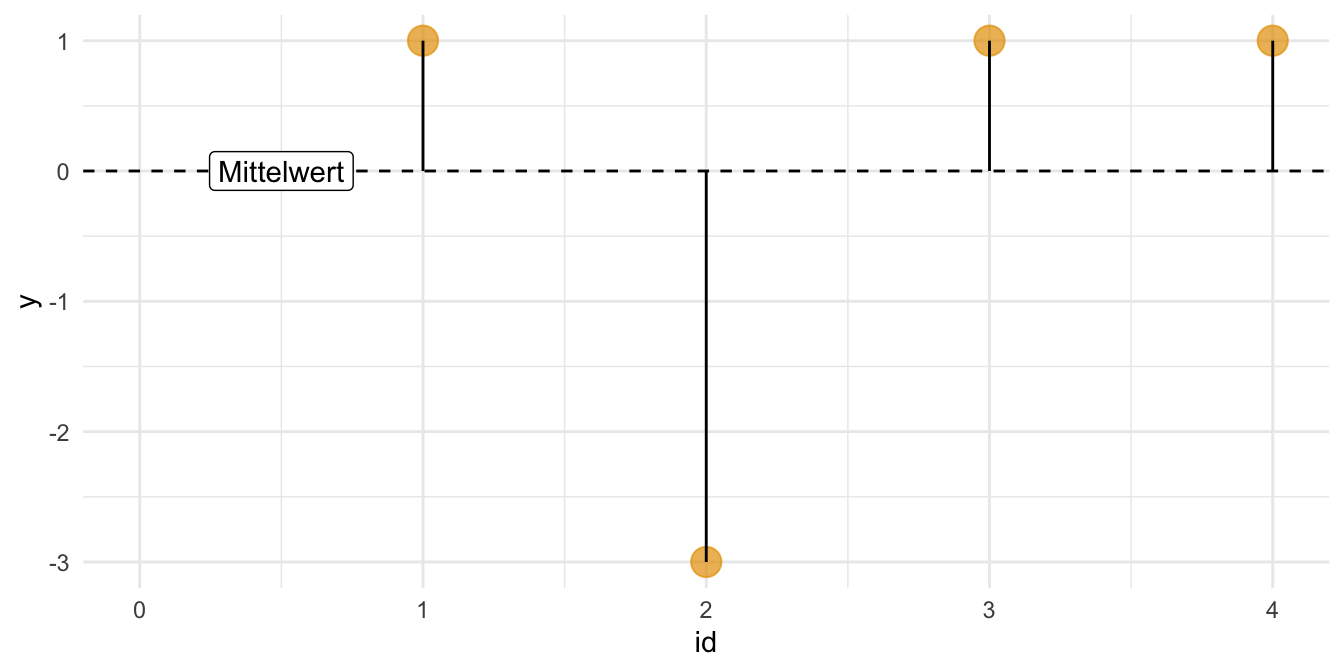
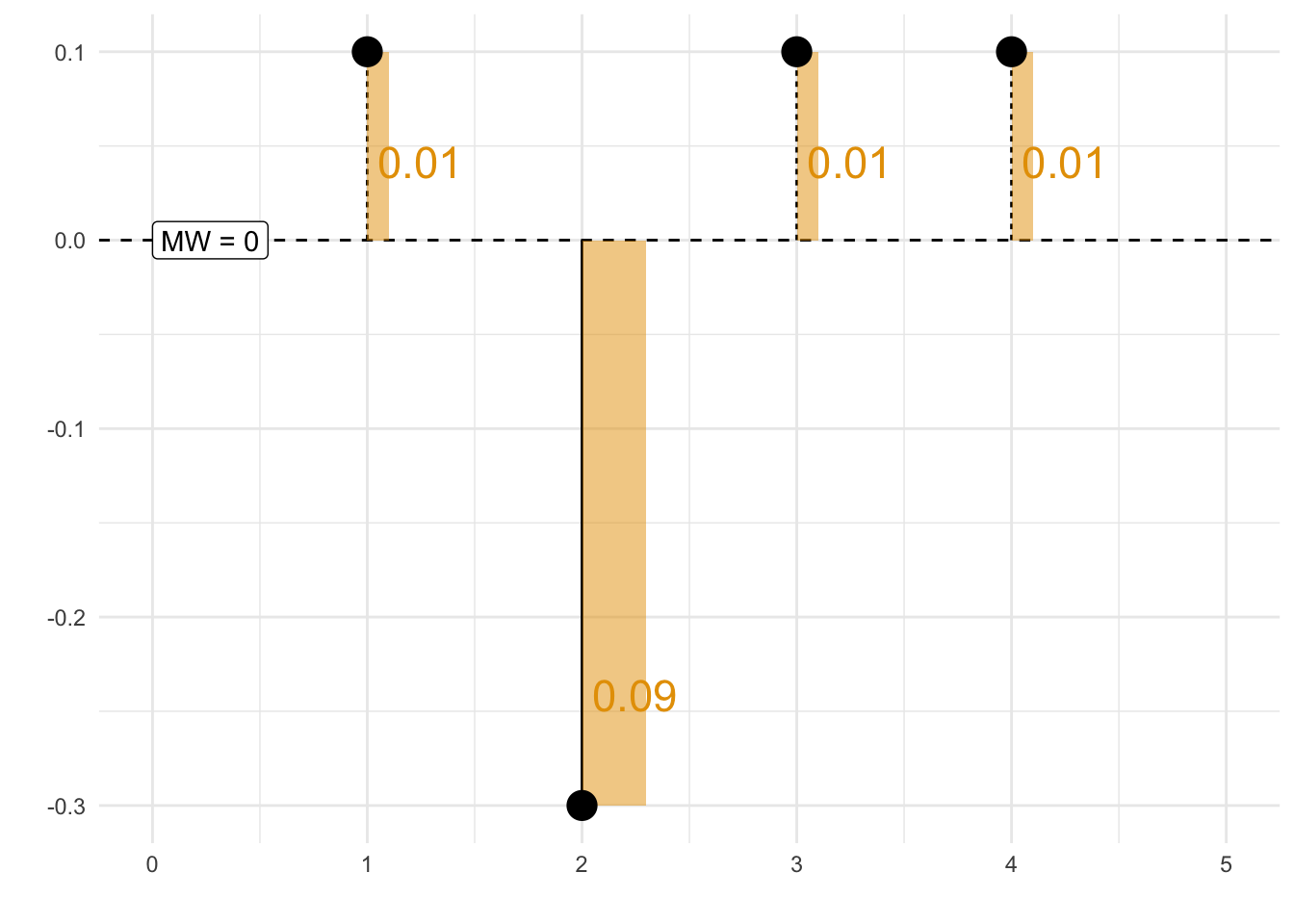
Beispiel 7.3 Abbildung 7.5 visualisiert ein einfaches Beispiel zum MAE. Rechnen wir den MAE für das Beispiel von Abbildung 7.5 aus:
\(MAE = \frac{1 + |- 3| + 1 + 1}{4} = 6/4 = 1.5 \; \square\)
Natürlich können wir R auch die Rechenarbeit überlassen.
🤖 Loving it!
Schauen Sie: Den Mittelwert (s. Abbildung 7.5) kann man doch mit Fug und Recht als ein lineares Modell, eine Gerade, betrachten, oder nicht? Schließlich erklären wir \(y\) anhand einer Gerade (die parallel zur X-Achse verläuft). In R gibt es einen Befehl, um ein lineares Modell zu berechnen, er heißt lm. Die Syntax von lm() lautet: lm(y ~ 1, data = meine_daten).
In Worten:
Hey R, berechne mit ein lineares Modell zur Erklärung von Y. Aber verwende keine andere Variable zur Erklärung von Y, sondern nimm den Mittelwert von Y.
lm_ohne_x_var <- lm(y ~ 1, data = d)Den MAE können wir uns jetzt so ausgeben lassen:
mae(lm_ohne_x_var) # aus dem Paket easystats
## [1] 1.57.3.2 Der Interquartilsabstand
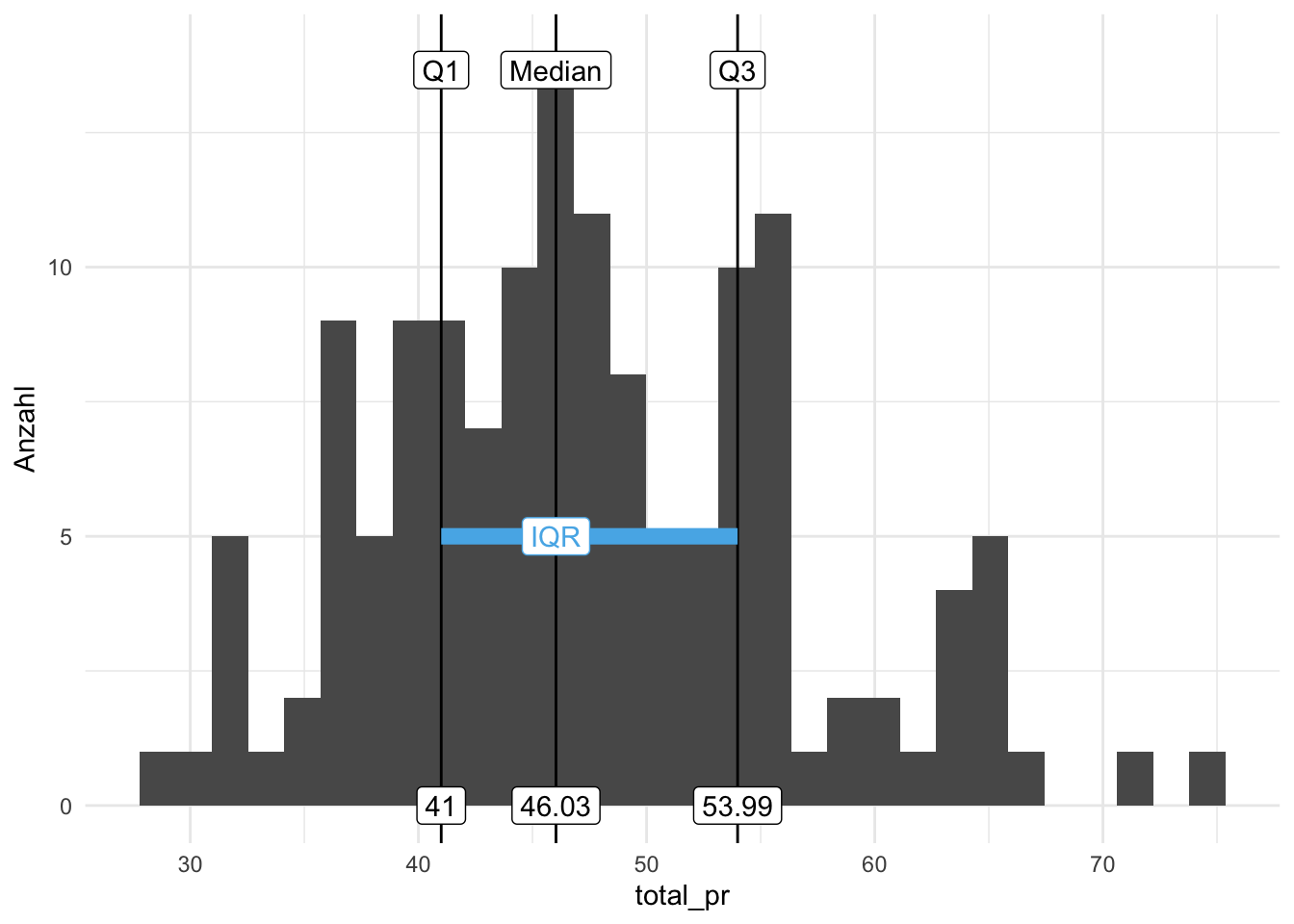
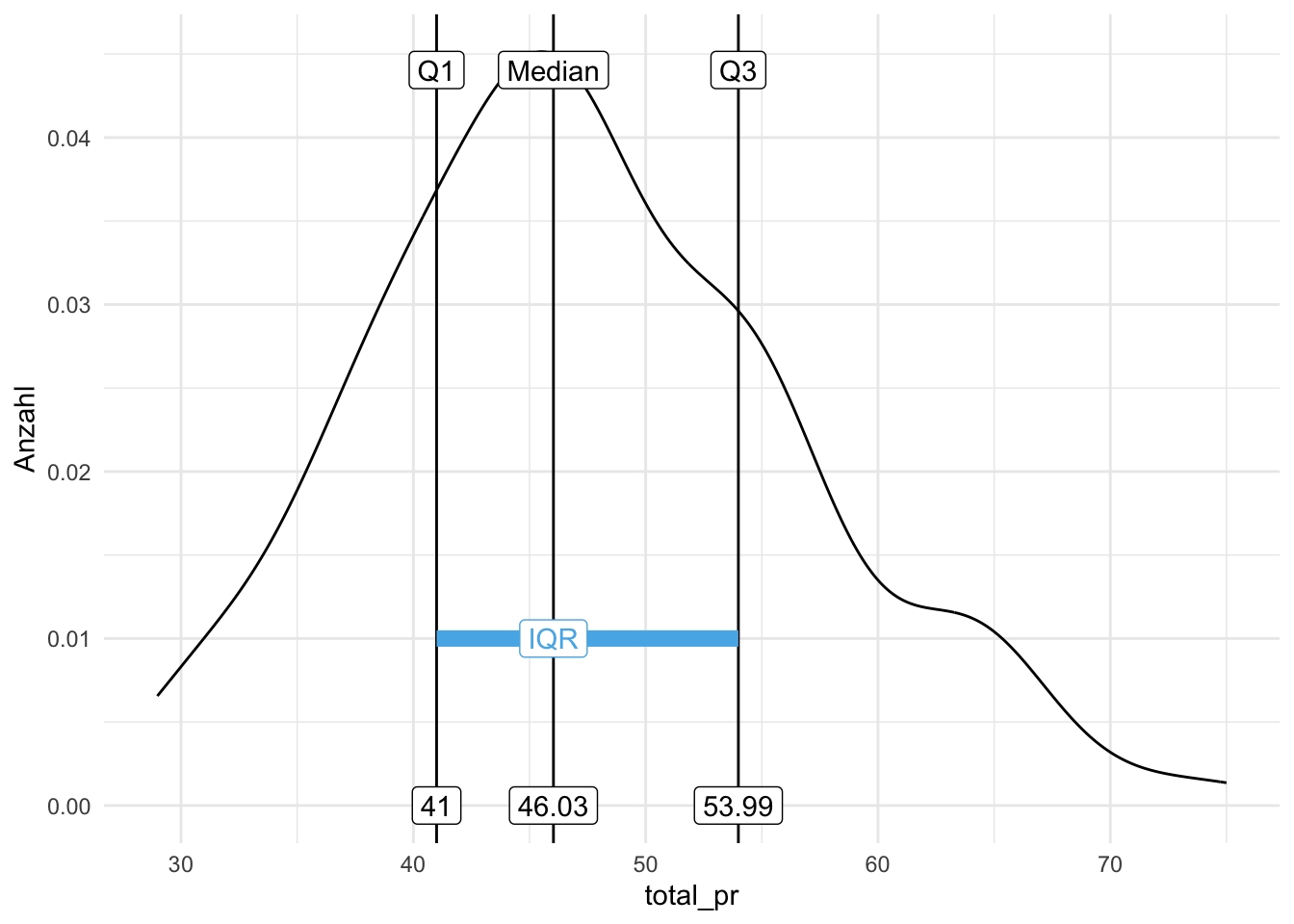
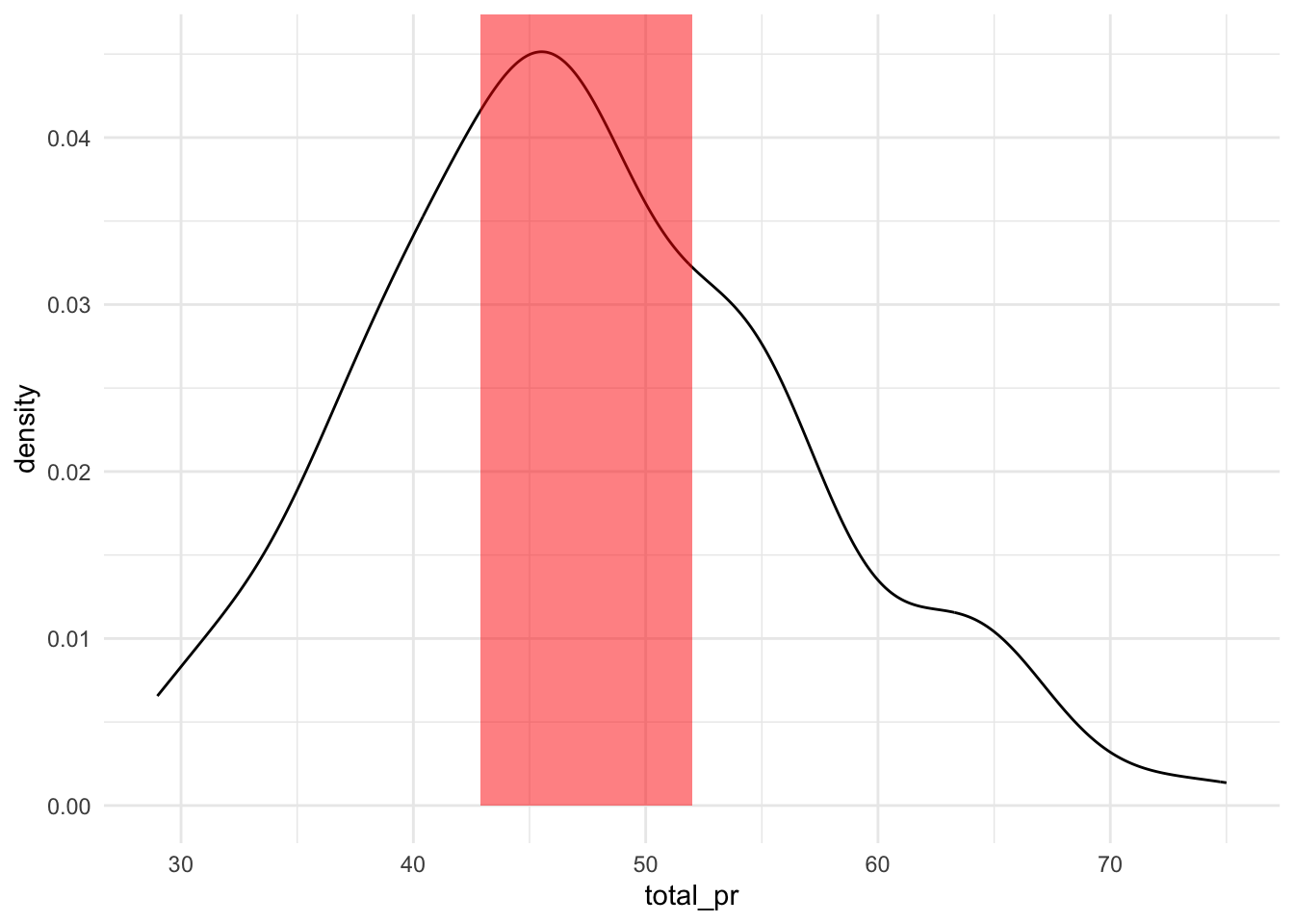
Der Interquartilsabstand (IQA; engl. inter quartile range, IQR) ist ein Streuungsmaß, das nicht auf dem Mittelwert aufbaut. Der IQR ist robuster als z.\(\,\)B. der MAA oder die Varianz und die Standardabweichung. Abbildung 7.6 stellt den IQR (und einige Quantile) für den Verkaufspreise von Mariokart-Spielen dar.
Definition 7.4 (Interquartilsabstand) Der Interquartilsabstand ist definiert als die (absolute) Differenz des 3. Quartils und 1. Quartils: \(IQR := Q_3-Q_1. \; \square\)
Beispiel 7.4 (IQR im Hörsaal) In einem Statistikkurs betragen die Quartile der Körpergröße: Q1: 1.65m, Q2 (Median): 1.70m, Q3: 1.75m. Der IQR beträgt dann: \(IQR = Q_3-Q_1 = 1.75\,m - 1.65\,m = 0.10\,m\), d.\(\,\)h. 10\(\,\)cm. \(\square\)
7.3.3 Streuungsmaße für Normalverteilungen
Normalverteilungen sind recht häufig anzutreffen in der Praxis der Datenanalyse. Daher lohnt es sich, zu überlegen, wie man diese Verteilungen kompakt zusammenfasst. Man kann zeigen, dass eine Normalverteilung sich komplett über ihren Mittelwert sowie ihre Standardabweichung beschreiben lässt (Lyon, 2014). Außerdem gilt: Sind Ihre Daten normalverteilt, dann sind die Abweichungen vom Mittelwert auch normalverteilt. Denn wenn man eine Konstante zu einer Verteilung addiert (bzw. subtrahiert), “verschiebt man den Berg” nur zur Seite, ohne die Form zu verändern, s. Abbildung 7.7.
Hat man normalverteilte Variablen, so ist die Standardabweichung (engl. standard deviation, SD, \(\sigma, s\)) eine geeignete Maßeinheit der Streuung, denn damit lässt sich die Streuung (Abweichung vom Mittelwert, Residuen) der Normalverteilung gut beschreiben.
🧑🎓 Aber wie berechnet man jetzt diese Standardabweichung?
🧑🏫 Moment, noch ein kurzer Exkurs zur Varianz …
🧑🎓 (seufzt)
7.3.4 Varianz
Die Varianz einer Variable (z.\(\,\)B. Verkaufspreis von Mariokart) ist der mittlere quadrierte Abstand jedes Verkaufspreises vom Mittelwert.
Abbildung 7.10 illustriert die Varianz als “mittlerer Quadratfehler”:
- Man gehe von der Häufigkeitsverteilung der Daten aus.
- Betrachtet man die Daten als Gewichte auf einer Wippe, so ist der Schwerpunkt der Wippe der Mittelwert.
- Man zeichnet für jeden Datenpunkt ein Quadrat mit einer Kantenlänge, die seinem Abstand zum Mittelwert entspricht.
- Diese Quadrate werden, wo nötig, in Rechtecke umgeformt (bei gleichbleibender Fläche) und so angeordnet, dass sie ein Rechteck mit den Seitenlängen \(n\) und \(\sigma^2\) bilden.
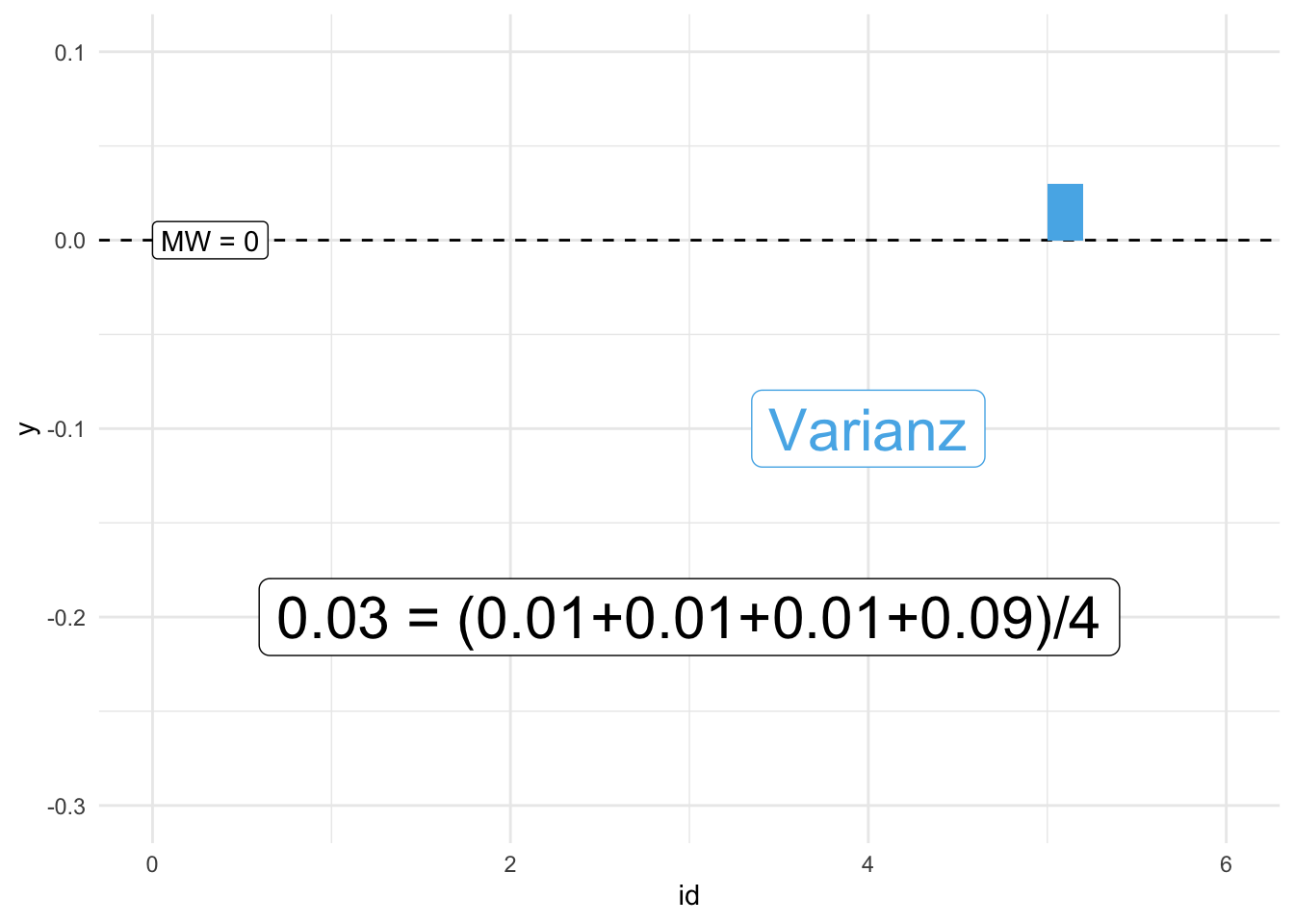
Abbildung 7.9 visualisiert die Varianz für Beispiel 7.3.1 Links sind die Abweichungsquadrate dargestellt, rechts die Varianz als “typisches Abweichungsquadrat”. Die Varianz ist also ein Maß, das die typische quadrierte Abweichung der Beobachtungen vom Mittelwert in eine Zahl fasst.
Beispiel 7.5 Sie arbeiten immer noch bei einem Online-Auktionshaus und untersuchen den Verkauf von Videospielen. Natürlich mit dem Ziel, dass Ihre Firma mehr von dem Zeug verkaufen kann. Dazu berechnen Sie die Streuung in den Verkaufspreisen, s. Listing 7.1 bzw. Tabelle 7.1. \(\square\)
Statistiken sind ja schön … aber Bilder sind auch gut, s. Abbildung 7.10. Datendiagramme eignen sich gut, um (grob) die Streuung einer Variable zu erfassen.
Wer sich die Berechnung von Hand für pr_maa sparen möchte (s. Listing 7.1), kann die Funktion MeanAD aus dem Paket DescTools nutzen. Um die Standardabweichung zu berechnen, berechnet man zunächst die Varianz, \(s^2\) abgekürzt. Hier ist ein “Kochrezept” (Algorithmus) zur Berechnung der Varianz:
- Für alle Datenpunkte \(x_i\): Berechne die Abweichungen vom Mittelwert, \(\bar{x}\).
- Quadriere diese Werte.
- Summiere dann auf.
- Teile durch die Anzahl \(n\) der Werte.
Als Formel ausgedrückt lautet die Definition der Varianz von \(Y\) bei einer Stichprobe der Größe \(n\) wie folgt, s. Gleichung 7.2. (Hier geht es um die sog. unkorrigierte Stichprobenvarianz; um anhand einer Stichprobe die Varianz der zugehörigen Population zu schätzen, teilt man nicht durch \(n\), sondern durch \(n-1\).)
\[{\displaystyle s^{2}:={\frac {1}{n}}\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}={\frac {1}{n}}\sum _{i=1}^{n}e_i^{2}.} \tag{7.2}\]
Definition 7.5 (Varianz) Die Varianz von \(Y\) (\(s^2, \sigma^2\)) ist definiert als der Mittelwert der quadrierten Abweichungen (vom Mittelwert von \(Y\)), \(e_i^2\). \(\square\)
Die Varianz steht im engen Verhältnis zur Kovarianz, s. Kapitel 8.3. Die Varianz kann auch verstehen als den mittleren Quadratfehler (Mean Squared Error, MSE) eines Modells, s. Gleichung 7.3.
\[{\displaystyle MSE:={\frac {1}{n}}\sum _{i=1}^{N}\left(y_{i}-{\hat {y}}\right)^{2}.} \tag{7.3}\]
Im Fall eines Punktmodells ist der Mittelwert der vorhergesagte Wert eines Modells: \(\hat{y} = \bar{y}\).
7.3.5 Die Standardabweichung
Definition 7.6 (Standardabweichung) Die Standardabweichung (SD, s, \(\sigma\)) ist definiert als die Quadratwurzel der Varianz, s. Gleichung 7.4.
\[s := \sqrt{s^2} \square \tag{7.4}\]
Kennt man die Varianz, so lässt sich die Standardabweichung einfach als Quadratwurzel der Varianz berechnen. Durch das Wurzelziehen besitzt die Standardabweichung wieder in etwa die gleiche Größenordnung wie die Daten (im Gegensatz zur Varianz, die durch das Quadrieren sehr groß werden kann). Die Standardabweichung ist also ein Maß, das grob (!) gesagt die “typische” Abweichung der Beobachtungen vom Mittelwert in eine Zahl fasst. Aus einem Modellierungsblickwinkel kann man die SD definieren als die Wurzel von MSE. Dann nennt man sie Root Mean Squared Error (RMSE): \(RMSE := \sqrt{MSE}\).
Die SD ist i.d.R. ungleich zur MAE, aber (fast) gleich zur RMSE. Entsprechend ist die Varianz (fast) gleich zur MSE. \(\square\)
Beispiel 7.6 Sie arbeiten weiter an Ihrem Mariokart-Projekt. Da Sie heute keine Lust auf viel Tippen haben, nutzen Sie das R-Paket easystats mit der Funktion describe_distribution, s. Tabelle 7.2.
describe_distribution (Auszug)
🧑🎓 Ah! Das war einfach. Reicht auch mal für heute. \(\square\)
Beispiel 7.7 Ihr Job als Datenanalyst ist anstrengend, aber auch mitunter interessant. So war auch der heutige Tag. Bevor Sie nach Hause gehen, möchten Sie noch eine Sache anschauen. In einer früheren Analyse (s. Abbildung 7.4) fanden Sie heraus, dass die Fehlerbalken kürzer werden, wenn man ein geschickteres und komplexeres Modell findet. Das wollen Sie natürlich prüfen. Sie überlegen: “Okay, ich will ein einfaches Modell, in dem der Mittelwert das Modell des Verkaufspreis sein soll.”
Das spezifizieren Sie so:
lm_mario_ohne_x_var <- lm(total_pr ~ 1, data = mariokart)
mae(lm_mario_ohne_x_var) # Modellgüte bzw. Modellfehler
## [1] 10Im nächsten Schritt spezifizieren Sie ein Modell, in dem der Verkaufspreis eine Funktion der Anzahl der Lenkräder ist (ähnlich wie in Abbildung 7.4):
lm_wheels <- lm(total_pr ~ wheels, data = mariokart)
mae(lm_wheels)
## [1] 7.4Ah! Sehr schön, Sie haben mit lm2 ein besseres Modell als einfach nur den Mittelwert gefunden. Ab nach Hause! \(\square\)
🧑🎓 Der “gesunde Menschenverstand” würde den mittleren Absolutabstand (MAA oder MAE) der Varianz (oder der Standardabweichung, SD) vorziehen. Warum brauche ich dann die SD?
🧑🏫 Ja, die MAA ist anschaulicher und insofern nützlicher als die Varianz und die SD. Wenn es nur um deskriptive Statistik geht, braucht man die Varianz (oder die SD) nicht unbedingt. Allerdings ist die SD nützlich zur Beschreibung der Normalverteilung. Außerdem wird die Varianz häufig verwendet bzw. in Forschungsarbeiten berichtet, daher hilft es Ihnen, wenn Sie die Varianz kennen. Liegen Extremwerte vor, kann es vorteilhafter sein, den IQR vorzuziehen gegenüber Mittelwert basierten Streuungsmaßen (MAA, Varianz, SD).
7.4 Streuung als Modellfehler
Wenn wir den Mittelwert als Punktmodell des Verkaufspreises auffassen, so kann man die verschiedenen Kennwerte der Streuung als verschiedene Kennwerte der Modellgüte auffassen.
Definieren wir zunächst als Punktmodell auf Errisch:
lm_mario_ohne_x_var <- lm(total_pr ~ 1, data = mariokart)Zur Erinnerung: Wir modellieren total_pr ohne UV (Prädiktoren), sondern als Punktmodell, und zwar schätzen wir den Mittelwert mit den Daten mariokart. Modelle ohne UV nennt man auch “Nullmodell”. Das (Meta-)Paket easystats bietet komfortable Befehle, um die Modellgüte zu berechnen:
mae(lm_mario_ohne_x_var) # Mean absolute error
mse(lm_mario_ohne_x_var) # Mean squared error
rmse(lm_mario_ohne_x_var) # Root mean squared error
## [1] 10
## [1] 655
## [1] 267.5 Die z-Transformation
Wenn man mit einem bestimmten Datensatz arbeitet, ist es häufig schwer zu sagen, welche Ausprägungen “groß” sind und welche “klein”. Um einzuschätzen zu können, welche Ausprägungen wie groß sind, sollte man die Quantile kennen. Dann kann man Aussagen machen wie “Ah, die Ausprägung X ist groß, weil 90 Prozent aller Leute einen kleineren Wert aufweisen”. Die z-Transformation hilft hier, dass sie die Werte in bekannte und verständliche Bereiche transformiert. So wird der Mittelwert auf Null transformiert und die Streuung (sd) auf 1. Bei normalverteilten Variablen weiß man dann direkt, dass der Mittelwert, Modus und Median bei Null sind, und ca. 98 Prozent der Werte kleiner als 2, s. Definition 5.6. Die z-Transformation besteht aus zwei Schritten: Zentrieren und (Streuung) standardisieren.
Sie arbeiten immer noch als Datenknecht, Moment, Datenhecht bei dem Online-Auktionshaus. Heute untersuchen Sie, wie gut sich die Verkaufspreise mit einer einzigen Zahl, dem mittleren Verkaufspreis, beschreiben lassen. Einige widerspenstige Werte haben Sie dabei einfach des Datensatzes verwiesen. Schon ist das Leben leichter, s. Listing 7.2.
7.5.1 Zentrieren
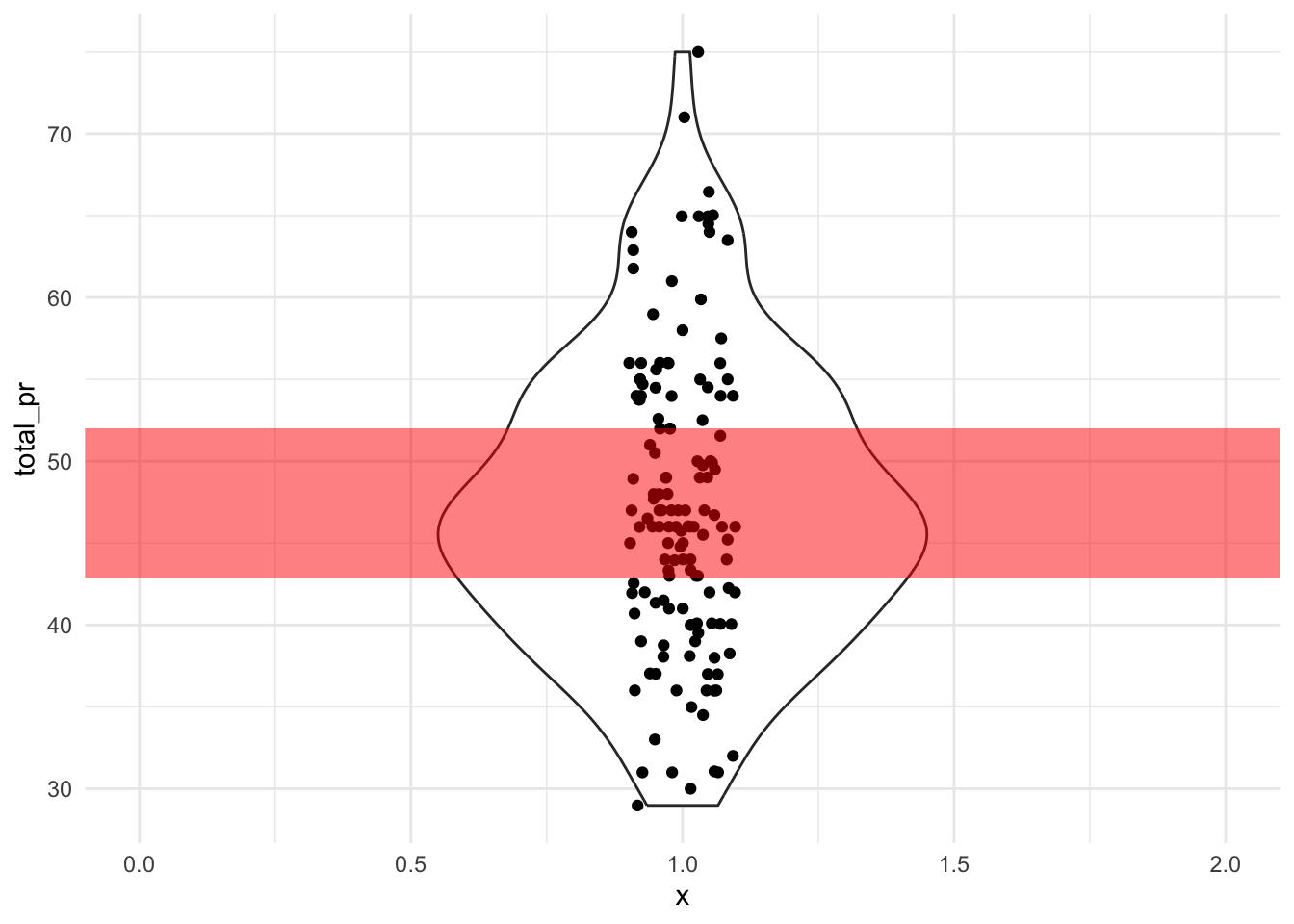
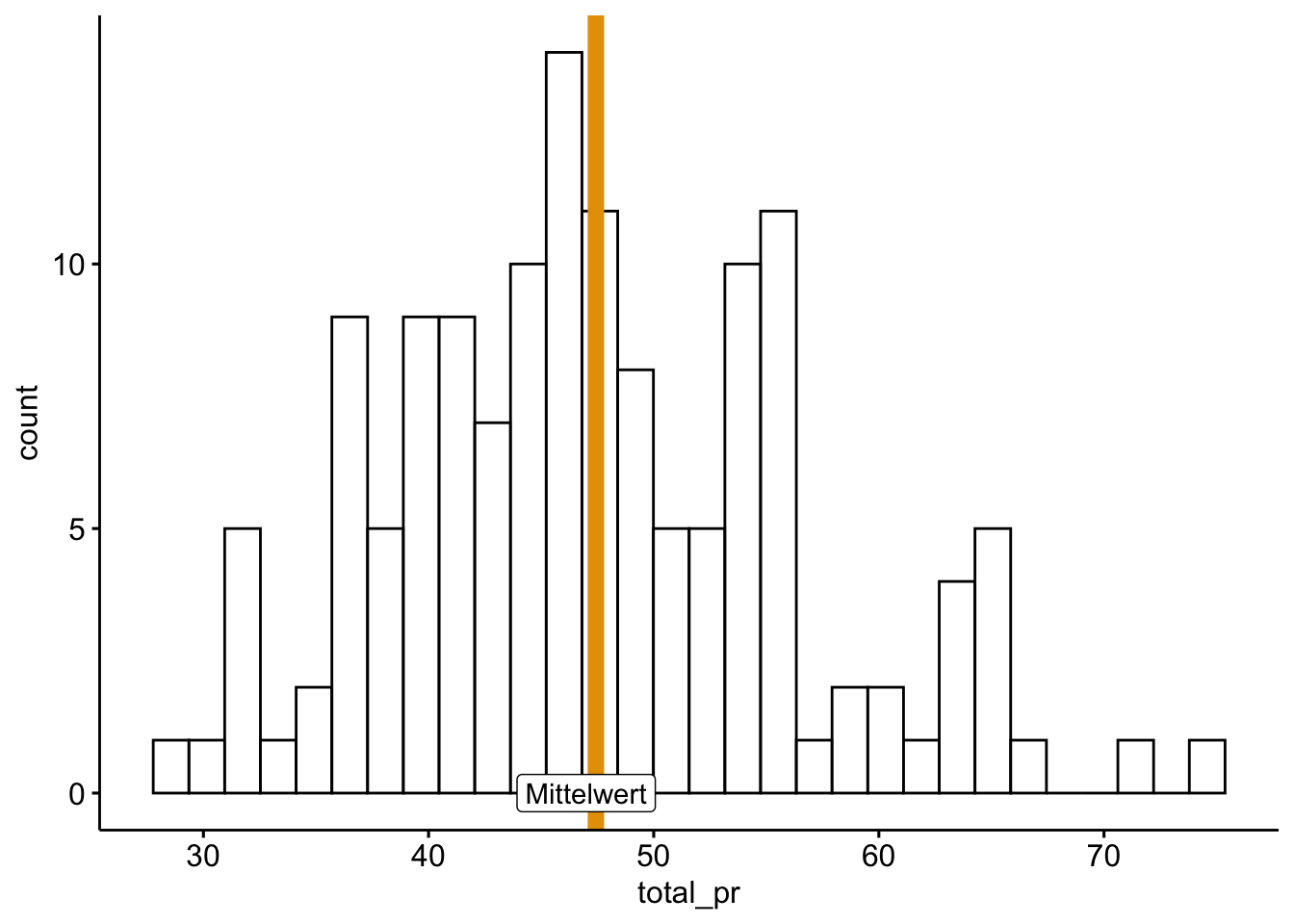
Abbildung 7.11 (rechts) zeigt die Verteilung; man sieht dass es einige Streuung um den Mittelwert (\(\bar{X}= 47\)) herum gibt. Abbildung 7.11 (links) zeigt die (um den Mittelwert) zentrierten Daten: Dort wurde von allen Werten der Mittelwert abgezogen.
mariokart_no_extreme; das Zentrieren ändert die Verteilung nicht, sondern ‘schiebt die Verteilung nur zur Seite’. Zentrierte Werte zeigen, wie weit die unzentrierten Werte von ihrem Mittelwert entfernt sind. Zentrieren erreicht man, indem von allen Werten den Mittelwert abzieht.
Man sieht, dass es eine gewisse Streuung um den Mittelwert herum gibt. Aber ist das viel oder wenig Streuung?
Je weniger Streuung um den Mittelwert herum, desto besser eignet sich der Mittelwert als Modell für die Daten und desto höher ist die Modellgüte.
Ja, es ist etwas Streuung, aber wie viel? Kann man das genau angeben? Sie überlegen … und überlegen. Da! Eine Idee!
Man könnte vielleicht angeben, wie viel Euro jedes Spiel vom Mittelwert entfernt ist. Je größer diese Abweichung, desto schlechter die Modellgüte! Also rechnen Sie diese Abweichung aus, Listing 7.3 und Tabelle 7.3.
total_pr zentriert: zentriert = total_pr - MW
| id | total_pr | MW | total_pr_zentriert |
|---|---|---|---|
| 1 | 52 | 47 | 3.8 |
| 2 | 37 | 47 | -10.7 |
| 3 | 46 | 47 | -2.2 |
| 4 | 44 | 47 | -3.7 |
| 5 | 71 | 47 | 23.3 |
| 6 | 45 | 47 | -2.7 |
Anders gesagt: Wir haben die Verkaufspreise zentriert.
Definition 7.7 (Zentrieren) Zentrieren bedeutet, von jedem Wert einer Verteilung \(X\) den Mittelwert zu subtrahieren: \(X_c = X - \bar{X}\). Daher ist der neue Mittelwert (der zentrierten Verteilung) gleich Null. \(\square\)
7.5.2 Streuung standardisieren
Aber irgendwie sind Sie noch nicht am Ziel Ihrer Überlegungen: Woher weiß man, ob 10 Euro oder 20 Euro “viel” Abweichung vom Verkaufspreis ist? Man müsste die Abweichung eines Verkaufspreises zu irgendetwas in Bezug setzen. Wieder! Ein Geistesblitz! Man könnte doch die jeweilige Abweichung in Bezug setzen zur mittleren (absoluten) Abweichung (MAA)! Ein alternativer, ähnlicher Kennwert zur MAA ist die SD. Sie haben gehört, dass die SD gebräuchlicher sei als die MAA. Um sich als Checker zu präsentieren, berechnen Sie also auch die SD; die beiden Koeffizienten sind ja ähnlich.
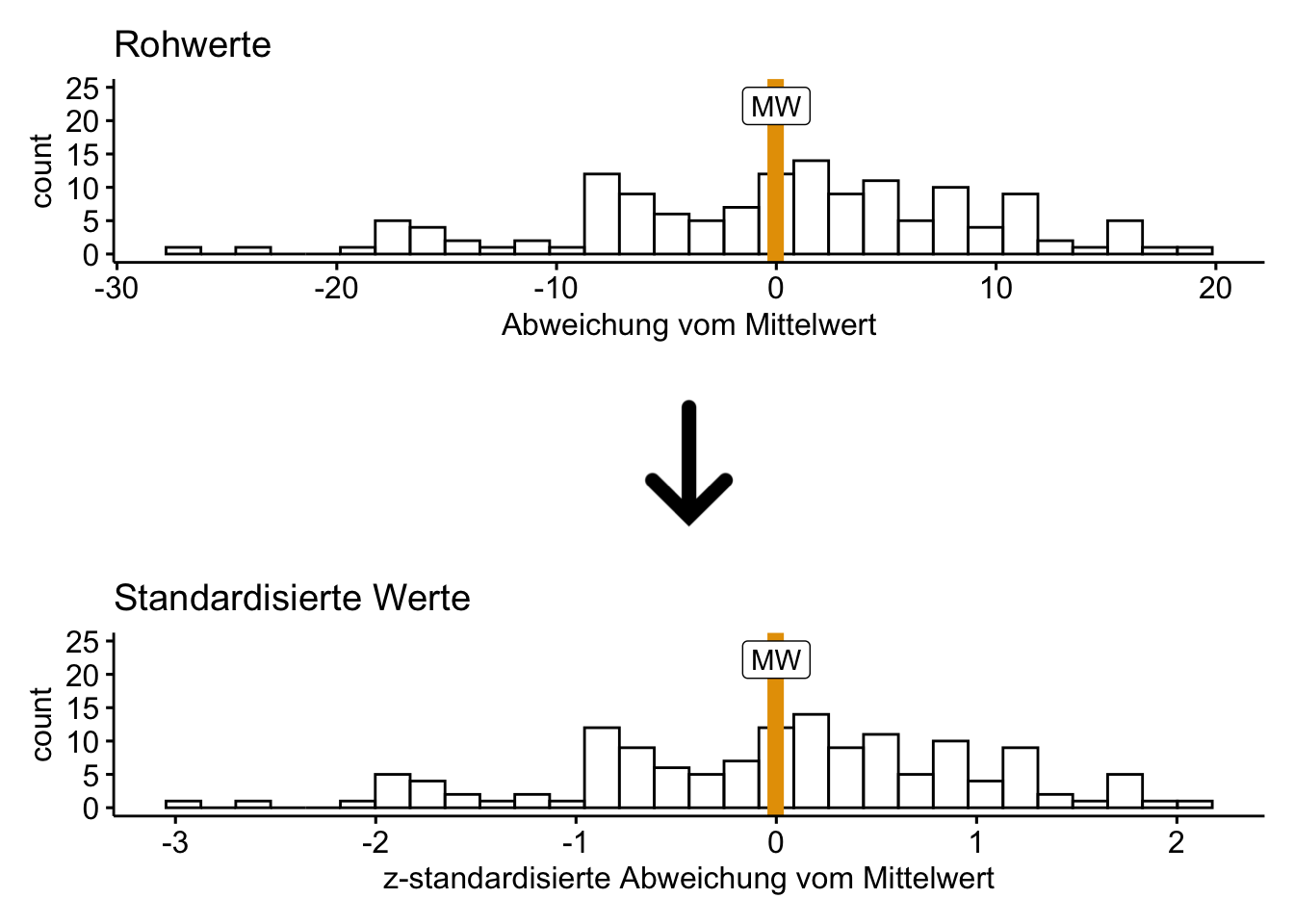
Also: Wenn ein Spiel 10 Dollar vom Mittelwert abweicht und die SD 10 Dollar betragen sollte, dann hätten wir eine “standardisierte” (abgekürzt manchmal mit std) Abweichung von 1, weil 10/10=1. Begeistert über Ihre Geistesblitze machen Sie sich ans Werk.
Zufrieden betrachten Sie Ihr Werk, s. Abbildung 7.12. In Abbildung 7.12 sieht man oben die Rohwerte und unten die transformierten Werte, die wir hier als z-standardisiert bezeichnen, da wir sie in Bezug zur “typischen Abweichung”, der SD, gesetzt haben.
7.5.3 z-Werte
Wir fassen die zwei Schritte unserer Umrechnung (“Transformation”) zusammen wie in einem Kochrezept:
- Berechne die Abweichungen vom mittleren Verkaufspreis (Differenz Mittelwert und jeweiliger Verkaufspreis)
- Teile die Abweichungen (aus Schritt 2) durch die SD
Fertig sind die z-Werte!
Diese Art von Transformation bezeichnet man als z-Transformation und die resultierenden Werte als z-Werte.
Definition 7.8 (z-Werte) z-Werte sind das Resultat der z-Transformation. Für die Variable \(X\) berechnet sich der z-Wert der \(i\)-ten Beobachtung so: \(z_i := \frac{x_i - \bar{x}}{sd_x}.\;\square\)
z-Werte sind nützlich, weil sie die “relative” Abweichung einzelner Beobachtungen vom Mittelwert anzeigen. Nach einer Faustregel spricht man von extremen Abweichungen (Extremwerten, Ausreißern), wenn \(z_i \ge 2.5\) (Shimizu, 2022).
Zentrieren bzw. z-tranformieren kann man sich mithilfe des R-Pakets easystats verrichten lassen:
mariokart_no_extreme_z_transformiert <-
mariokart_no_extreme |>
mutate(total_pr_zentriert = as.numeric(center(total_pr)),
total_pr_z_transformiert = as.numeric(standardise(total_pr)))Definition 7.9 (Standardnormalverteilung) Eine Standardnormalverteilung ist eine Normalverteilung mit Mittelwert von 0 und einer Standardabweichung von 1. Man schreibt kurz: \(X \sim \mathcal{N}(0, 1)\quad \square\).
Man kann jede Normalverteilung in eine Standardnormalverteilung überführen mit der z-Transformation.
7.6 Quiz
Was ist das mathematische Resultat, wenn man alle (nicht-absoluten) Residuen einer Verteilung vom Mittelwert aufsummiert? Betrachten Sie die Eigenschaft des Mittelwerts als Schwerpunkt.
Da der Mittelwert der Schwerpunkt einer Verteilung ist, gleichen sich positive und negative Abweichungen exakt aus. Die Summe der einfachen Residuen ist daher immer Null.
- Falsch
- Richtig
- Falsch
- Falsch
- Falsch
Sie haben ein Modell lm1 (nur Mittelwert) und ein Modell lm2 (mit einer UV). In R liefert mae(lm1) den Wert 10 und mae(lm2) den Wert 7,4. Wie beurteilen Sie die Veränderung der Modellgüte?
Ein geringerer MAE bedeutet kürzere Fehlerbalken. Je kleiner der Fehler, desto höher ist die Modellgüte.
- Falsch
- Falsch
- Richtig
- Falsch
- Falsch
In R berechnen Sie für ein Nullmodell (Punktmodell) den RMSE. Welcher statistische Kennwert der abhängigen Variable entspricht diesem Ergebnis (nahezu) exakt? Berücksichtigen Sie die Definition des RMSE im Kontext des Mittelwerts.
Beim Nullmodell ist der Vorhersagewert der Mittelwert. Die Wurzel aus dem mittleren quadrierten Fehler (RMSE) ist dann mathematisch äquivalent zur Standardabweichung.
- Falsch
- Falsch
- Falsch
- Richtig
- Falsch
Ein Student hat in einem Statistiktest einen z-Wert von -2,0 erzielt. Wie ist dieses Ergebnis im Vergleich zur restlichen Gruppe zu interpretieren? Nutzen Sie die Definition von z-Werten als relative Abweichungen.
Ein z-Wert gibt an, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist. Ein negatives Vorzeichen bedeutet, dass der Wert unter dem Durchschnitt liegt.
- Falsch
- Falsch
- Falsch
- Falsch
- Richtig
Was passiert bei einer z-Transformation mit dem Mittelwert und der Standardabweichung einer beliebigen Verteilung? Die Transformation besteht aus Zentrieren und Standardisieren.
Durch das Abziehen des Mittelwerts (Zentrieren) verschiebt sich das Zentrum auf 0. Durch das Teilen durch die SD wird die Streuung auf 1 normiert.
- Falsch
- Falsch
- Richtig
- Falsch
- Falsch
Ein Datensatz weist einen sehr extremen Ausreißer auf. Welches Streuungsmaß ist in dieser Situation am ehesten zu empfehlen, um ein verzerrtes Bild zu vermeiden? Nutzen Sie das Konzept der Robustheit.
Der IQR basiert auf Quantilen (Q3 - Q1) und ignoriert die extremen Ränder der Verteilung. Dadurch bleibt er stabil, selbst wenn einzelne Werte extrem abweichen.
- Richtig
- Falsch
- Falsch
- Falsch
- Falsch
Warum wird in der Statistik die Standardabweichung (SD) oft der Varianz vorgezogen, wenn es um die Beschreibung von Daten geht? Betrachten Sie die mathematische Transformation bei der Berechnung der SD. Überlegen Sie, was mit der Maßeinheit der Daten passiert.
Die Varianz nutzt quadrierte Abweichungen, was die Einheit verändert (z. B. Quadrat-Euro). Durch das Wurzelziehen bei der SD kehrt man zur ursprünglichen Einheit (z. B. Euro) zurück.
- Falsch
- Falsch
- Richtig
- Falsch
- Falsch
Vier Abweichungen von einem Mittelwert betragen: 1, -3, 1 und 1. Wie hoch ist der Mean Absolute Error (MAE) für diese Daten? Wenden Sie die Definition der mittleren Absolutabweichung an. Beachten Sie den Umgang mit negativen Vorzeichen.
Der MAE berechnet sich aus der Summe der Absolutbeträge der Fehler geteilt durch n. Hier: (1 + 3 + 1 + 1) / 4 = 6 / 4 = 1,5.
- Falsch
- Falsch
- Richtig
- Falsch
- Falsch
Sie betrachten ein einfaches Punktmodell für Klausurnoten. Nun erweitern Sie das Modell, indem Sie die Studierenden in zwei Gruppen (viel gelernt vs. wenig gelernt) aufteilen. Was passiert im Idealfall mit den Residuen (Fehlerbalken) im Vergleich zum ungruppierten Modell? Denken Sie an die grafische Darstellung der Abweichungen in Teilsamples.
Durch ein komplexeres Modell (Gruppierung) passen sich die Vorhersagen besser an die Daten an. Dies führt dazu, dass die Abweichungen der beobachteten Werte von den (gruppenbezogenen) Modellwerten sinken.
- Falsch
- Falsch
- Falsch
- Richtig
- Falsch
Zwei Medikamente zur Gewichtsreduktion zeigen in einer Studie den exakt gleichen mittleren Effekt. Bei Präparat A ist die Streuung der individuellen Ergebnisse jedoch minimal. Bei Präparat B ist die Streuung der Ergebnisse extrem hoch. Welche Aussage zur Modellgüte des Mittelwerts ist in diesem Fall korrekt? Betrachten Sie die Verlässlichkeit der Vorhersage für eine einzelne Person.
Ein gutes Modell zeichnet sich durch geringe Fehlerbalken (Residuen) aus. Geringe Streuung bedeutet, dass der Mittelwert die einzelnen Beobachtungen gut repräsentiert.
- Falsch
- Falsch
- Falsch
- Falsch
- Richtig
7.7 Aufgaben
Die Webseite datenwerk.netlify.app stellt eine Reihe von einschlägigen Übungsaufgaben bereit. Sie können die Suchfunktion der Webseite nutzen, um die Aufgaben mit den folgenden Namen zu suchen:
- mariokart-sd2
- mariokart-sd3
- Kennwert-robust
- summarise04
- summarise05
- vis-mariokart-variab
- sd-vergleich
- nasa01
- Streuung-Histogramm
- mariokart-sd1
- summarise06
- mariokart-desk01
Übungsaufgabe 7.2 (Analysieren Sie den Datensatz zur Handynutzung)
Die Forschungsfrage einer Studie fragt, ob Handynutzung die Konzentrationsfähigkeit verringert. Nehmen Sie ggf. an der Studie (Umfrage) teil (sie ist anonym und dauert drei Minuten).
Laden Sie den Datensatz zur Handynutzung von Google-Docs herunter.2 Berechnen Sie dann gängige deskriptive Statistiken und visualisieren Sie sie. \(\square\)
Lösung: Daten importieren
Sie können die Daten entweder selber herunterladen oder aber die folgende Version des Datensatzes verwenden. In beiden Fällen ist es nützlich, den (absoluten oder relativen) Pfad anzugeben:
data_path <- "https://raw.githubusercontent.com/sebastiansauer/statistik1/main/data/Smartphone-Nutzung%20(Responses)%20-%20Form%20responses%201.csv"Dann können Sie die Daten wie gewohnt importieren:
smartphone_raw <- read.csv(data_path)Lösung: Daten aufbereiten
Die Spaltennamen sind sehr unschön. Lassen Sie uns daher die Spaltennamen umbenennen (aber vorab sichern):
Check:
glimpse(smartphone_raw)
## Rows: 70
## Columns: 18
## $ item1 <chr> "21/03/2024 15:36:52", "05/04/2024 10:24:58", "05/04/2024 10…
## $ item2 <chr> "15:31:00", "10:23:00", "10:40:00", "11:14:00", "12:33:00", …
## $ item3 <int> 3, 4, 3, 3, 5, 5, 5, 5, 1, 2, 5, 3, 2, 2, 2, 5, 3, 1, 2, 4, …
## $ item4 <int> 5, 3, 3, 3, 4, 3, 3, 6, 2, 4, 5, 1, 1, 2, 3, 3, 4, 3, 2, 4, …
## $ item5 <int> 3, 3, 1, 5, 1, 3, 2, 4, 3, 2, 1, 1, 1, 4, 1, 2, 2, 1, 1, 1, …
## $ item6 <int> 4, 2, 4, 3, 5, 4, 6, 3, 2, 5, 6, 4, 2, 6, 5, 5, 5, 5, 5, 4, …
## $ item7 <int> 4, 3, 2, 3, 3, 1, 3, 2, 1, 2, 1, 1, 1, 3, 2, 2, 1, 2, 2, 2, …
## $ item8 <int> 1, 3, 1, 2, 3, 1, 1, 2, 2, 2, 1, 1, 2, 4, 1, 1, 2, 2, 1, 2, …
## $ item9 <int> 2, 6, 1, 3, 6, 5, 5, 2, 2, 5, 6, 1, 1, 5, 4, 6, 2, 4, 3, 4, …
## $ item10 <int> 2, 5, 5, 3, 4, 3, 1, 5, 1, 5, 3, 4, 3, 5, 4, 4, 4, 5, 3, 2, …
## $ item11 <int> 5, 6, 6, 5, 6, 6, 5, 6, 4, 3, 6, 4, 4, 5, 3, 6, 6, 4, 4, 5, …
## $ item12 <int> 1, 3, 1, 2, 5, 2, 4, 2, 1, 1, 3, 1, 1, 1, 1, 1, 3, 1, 1, 2, …
## $ item13 <int> 4, 3, 4, 2, 4, 2, 5, 3, 1, 1, 4, 1, 3, 4, 1, 3, 5, 2, 1, 4, …
## $ item14 <chr> "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", …
## $ item15 <chr> "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", …
## $ item16 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
## $ item17 <chr> "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", …
## $ item18 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …7.7.1 Komplette Lösung
😁
7.7.2 Fallstudie zur Lebenszufriedenheit
Die OECD führt eine weltweite Studie zur Lebenszufriedenheit durch.3 Arbeiten Sie die die Fallstudie “oecd-yacsda” im Datenwerk durch, um ein tieferes Verständnis für die Lebenszufriedenheit in verschiedenen Ländern der Welt zu bekommen.
7.8 Literaturhinweise
Allen Downey (2023) stellt in seinem vergnüglich zu lesenden Buch eine kurzweilige Einführung in die Statistik vor; auch Streuungsmaße haben dabei einen Auftritt. Wer mehr “Lehrbuch-Feeling” sucht, wird bei Çetinkaya-Runde & Hardin (2021) fündig (das Buch ist online frei verfügbar). Es ist kein Geheimnis, dass Streuungsmaße keine ganz neuen Themen in der Statistik sind. Aber hey, Oldie is Goldie, ohne Streuungsmaße geht’s nicht. Jedenfalls werden Sie in jedem Statistik-Lehrbuch, dass Sie in der Bib (oder sonst wo) aus dem Regal ziehen, fündig werden zu diesem Thema. Die Bücher unterscheiden sich meist “nur” in ihrem Anspruch bzw. der didaktischen Aufmachung; für jeden Geschmack ist da was dabei.
Die Abweichungsquadrate wirken optisch nicht quadratisch, da die X-Achse breiter skaliert dargestellt ist als die Y-Achse. Trotzdem sind es Quadrate, nur nicht optisch, wenn Sie wissen, was ich meine …↩︎
https://docs.google.com/spreadsheets/d/1SWMj4rIIIJdAsfsSKQHSg8jHr_OuKLpJx_0XV4LGnH0/edit?usp=sharing↩︎
https://www.oecd.org/wise/measuring-well-being-and-progress.htm↩︎