8  Punktmodelle 2

Schlüsselwörter

Statistik, Prognose, Modellierung, R, Datenanalyse, Regression

8.1 Einstieg

In diesem Kapitel benötigen Sie die üblichen R-Pakete (tidyverse, easystats) und Daten (mariokart), s. Kapitel 3.7.3 und Kapitel 3.4.

8.1.1 Lernziele

• Sie können die Begriffe Kovarianz und Korrelation definieren und ihren Zusammenhang erläutern.
• Sie können die Stärke einer Korrelation einschätzen.

library(tidyverse)
library(easystats)

mariokart <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/openintro/mariokart.csv")

8.1.2 Zum Einstieg

Übungsaufgabe 8.1  

1. Suchen Sie sich eine vertrauenswürdige Partnerin oder einen vertrauenswürdigen Partner. Im Zweifel reicht die erste Person, die Sie sehen. 😁
2. Fragne Sie diese Person nach je zwei Variablen, die wie folgt zusammenhängen:

• gleichsinnig (Viel von dem einen, viel von dem anderen)
• gegensinnig (viel von dem einen, wenig von dem anderen)
• Scheinzusammenhang (hängt zusammen, ist aber nicht “echt” bzw. kausal) $◻$

8.2 Zusammenfassen zum Zusammenhang

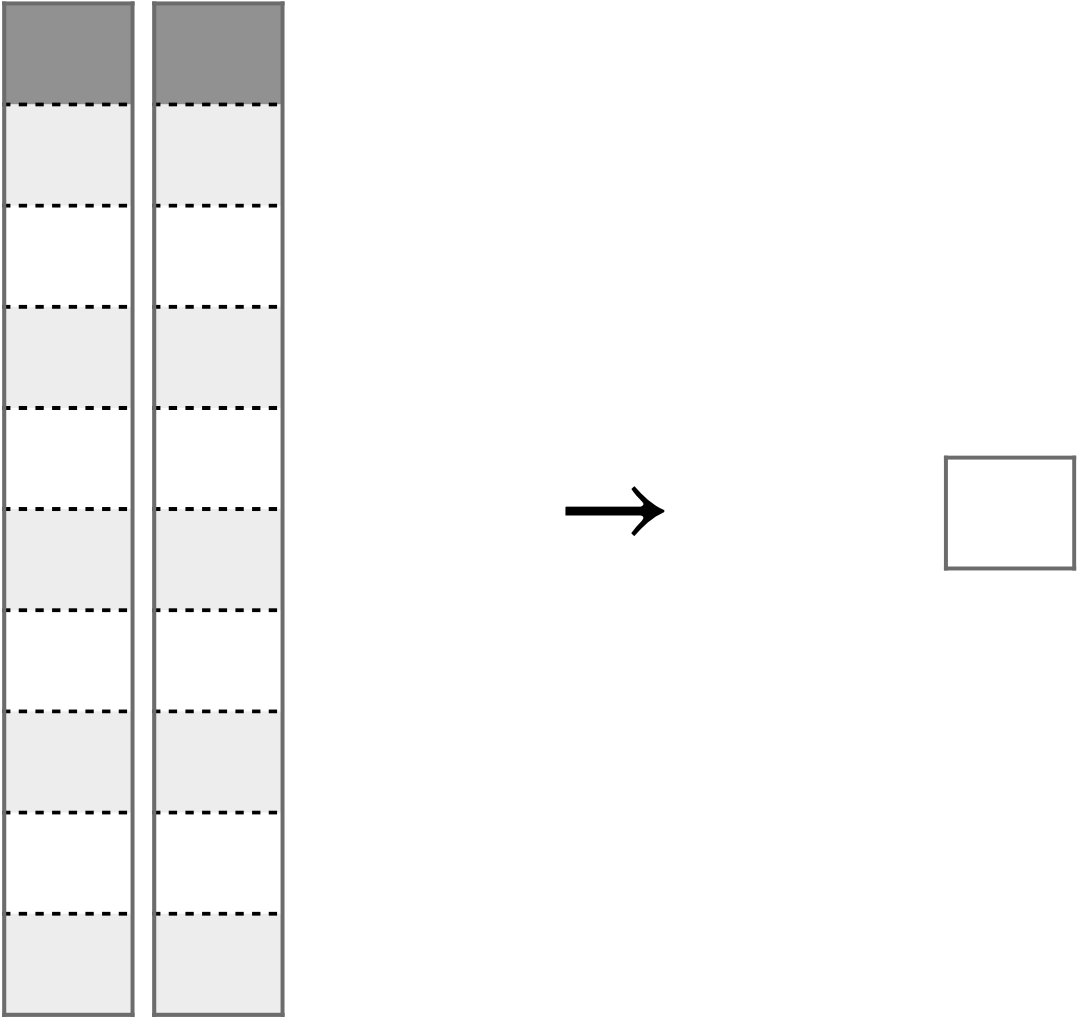
In Kapitel 6 haben wir gelernt, dass das Wesen eines Punktmodells als Zusammenfassung einer Spalte (eines Vektors) zu einer einzelnen Zahl, zu einem “Punkt” sozusagen, zusammengefasst werden kann. In diesem Kapitel fassen wir zwei Spalten zusammen, wieder zu einer Zahl, s. Abbildung 8.1. Während wir in Kapitel 6 eine Variable mit Hilfe eines Lagemaßes beschrieben (bzw. dargestellt, zusammengefasst, modelliert) haben, tun wir hier das Gleiche für zwei Variablen. Beschreibt man aber zwei Variablen, so geht es um die Frage, was die beiden Variablen miteinander zu tun haben: Wie die beiden Variablen voneinander (statistisch) abhängen bzw. miteinander (in welcher Form auch immer) zusammenhängen. Wir begrenzen uns auf metrische Variablen.

Abbildung 8.1: Zwei Spalten werden zu einer Zahl zusammengefasst

Die Verbildlichung (Visualisierung) zweier metrischer Variablen haben wir bereits in Kapitel 5.6.2 kennengelernt. Zur Verdeutlichung wie ein Zusammenhang zweier metrischer Variablen aussehen kann, hilft noch einmal Abbildung 8.2.

(a) Streudiagramm mit Trendlinie

 

(b) Verwackeltes Streudiagramm

Abbildung 8.2: Visualisierung des Zusammenhangs von wheels und total_pr. (a) Streudiagramm mit Trendlinie (und Ellipse zur Verdeutlichung). (b) ‘Verwackeltes’ Streudiagramm, um die einzelnen Punkte besser zu erkennen

8.3 Abweichungsrechtecke

Die Stärke des linearen Zusammenhangs zweier metrischer Variablen kann man gut mithilfe von Abweichungsrechtecken veranschaulichen. Los geht’s!

8.3.1 Noten und Abweichungsrechtecke

Beispiel 8.1 (Wieder Statistiknoten) Anton, Bert, Carl und Daniel haben ihre Statistikklausur zurückbekommen. Die Lernzeit $X$ scheint mit der erreichten Punktzahl $Y$ (0-100, je mehr desto besser) zusammenzuhängen.¹ Gar nicht so schlecht ausgefallen wie gedacht …, s. Tabelle 8.1. $◻$

Tabelle 8.1: Punkte in der Statistikklausur (x, 0-100) und Lernzeit (y, 0-100)

id	y	x
1	72	70
2	44	40
3	39	35
4	50	67

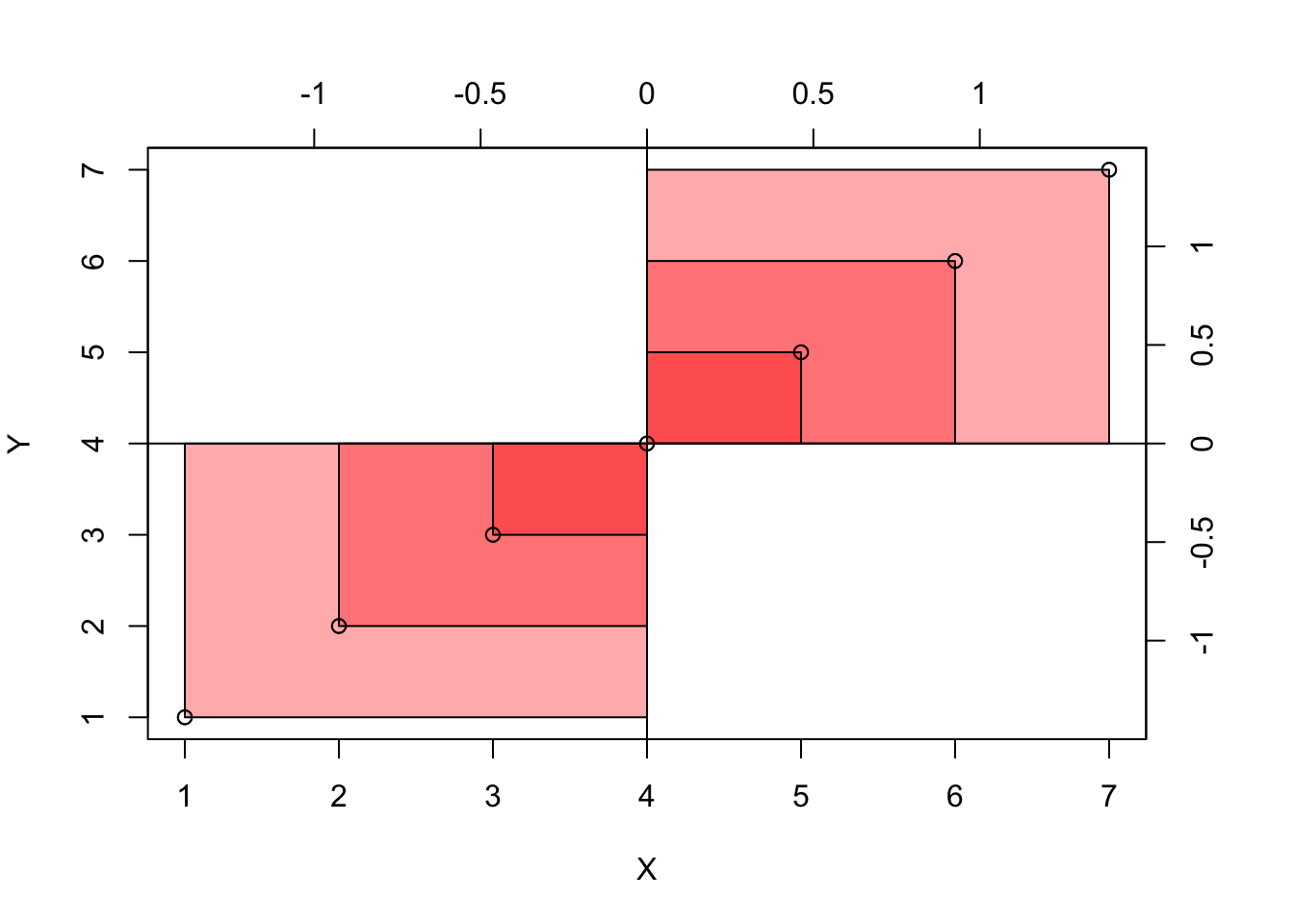
Zeichnen wir uns die Daten als Streudiagramm, s. Abbildung 8.3. Dabei zeichnen wir noch Abweichungsrechtecke ein.

Definition 8.1 (Abweichungsrechteck) Im zweidimensionalen Fall spannt sich ein Abweichungsrechteck vom Mittelwert $\overline{x}$ bis zum Messwert $x_i$ und genauso für $Y$. Wir bezeichnen mit $d{x}_i$ die Distanz (Abweichung) vom Mittelwert $\overline{x}$ bis zum Messwert $x_i$ (und analog $d{y}_i$), also $d{x}_i=x_i-\overline{x}$. Die Fläche des Abweichungsrechtecks ist dann das Produkt der Abweichungen: $d{x}_i\cdot d{y}_i$. $◻$

Abbildung 8.3: Die Kovarianz als mittleres Abweichungsrechteck. In jedem der vier Quadranten (Q1, Q2, Q3, Q4) ist das Vorzeichen der Abweichungsrechtecke dargestellt. Die Farben der Abweichungsrechtecke spiegeln das Vorzeichen wider.

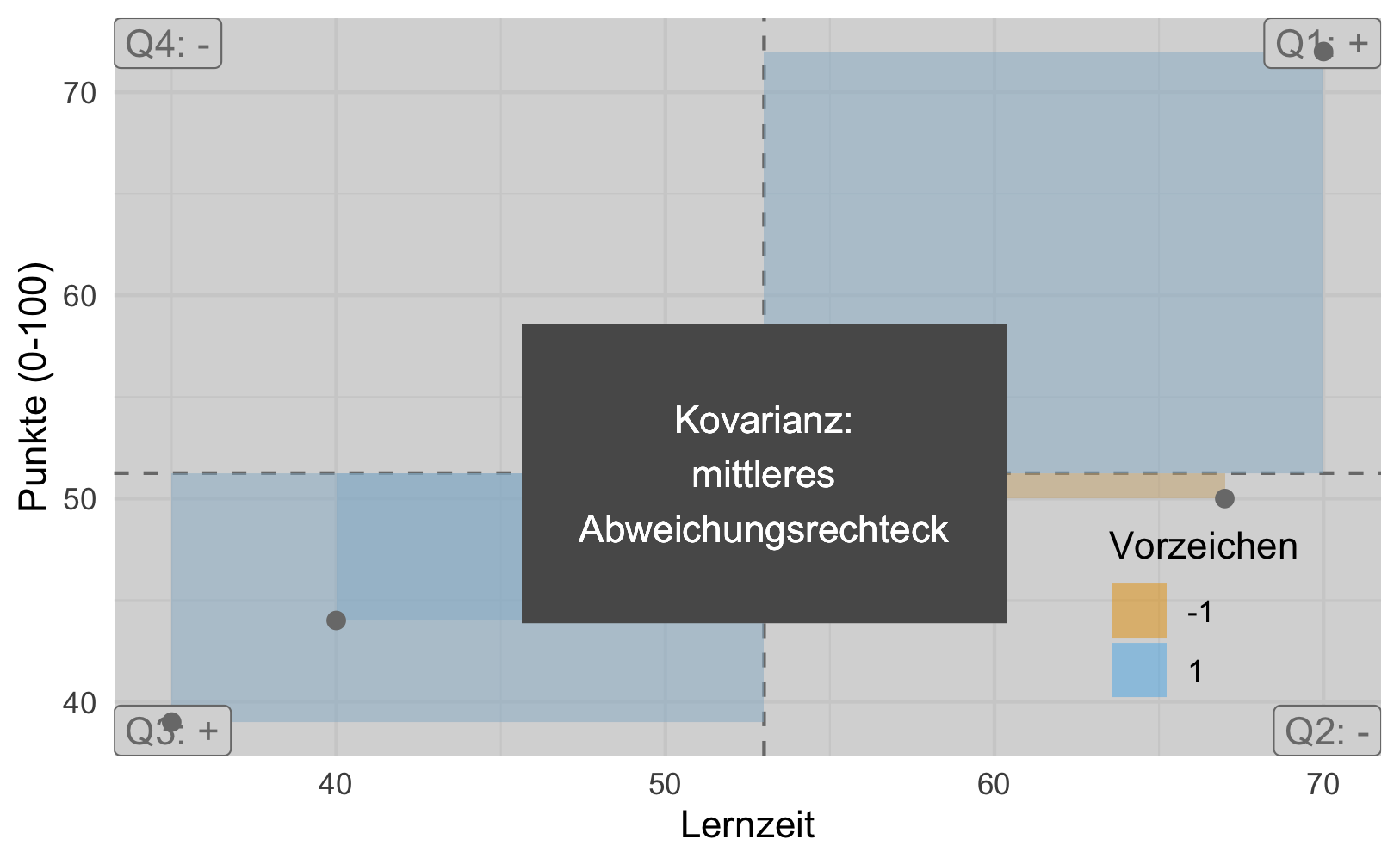
Stellen Sie sich vor, wir legen alle Rechtecke zusammen aus Abbildung 8.3. Nennen wir das resultierende Rechteck das “Summenrechteck”. Ja, ich weiß, ich strapaziere mal wieder Ihre Phantasie. Jetzt kommt’s: Je größer die Fläche des Summenrechtecks ist, desto stärker der (lineare) Zusammenhang. Beachten Sie, dass die Flächen Vorzeichen haben, positiv oder negativ (Plus oder Minus), je nachdem, in welchem der vier Quadranten sie stehen. Die Füllfarben der Rechtecke verdeutlichen dies, s. Abbildung 8.3. Das Vorzeichen der Summe zeigt an, ob der Zusammenhang positiv (gleichsinnig, ansteigende Trendlinie) oder negativ (gegensinnig, absinkende Trendlinie) ist. So zeigt Abbildung 8.4 links eine positive Summe der Abweichungsrechtecke und rechts eine negative Summe. Man sieht im linken Teildiagramme, dass die Summe der Rechtecke mit positivem Vorzeigen (oben-rechts und unten-links) überwiegt; im rechten Teildiagramm ist es umgekehrt: Die Rechtecke in Quadranten mit negativem Vorzeichen überwiegen (oben-links und unten-rechts).

(a) Positive Vorzeichen (Quadranten rechts-oben und links-unten) überwiegen, was in einer positiven Kovarianz resultiert

 

(b) Negative Vorzeichen (Quadranten links-oben und rechts-unten) überwiegen, was in einer negativen Kovarianz resultiert

Abbildung 8.4: Positive und negative Kovarianz: Einmal resultiert eine positive Summe, einmal eine negative Summe, wenn man die Flächen der Abweichungsrechtecke addiert.

Wir können das Summenrechteck noch durch die Anzahl der Datenpunkte teilen, das ändert nichts an der Aussage, aber der Mittelwert hat gegenüber der Summe den Vorteil, dass er in seiner Aussage unabhängig ist von der Anzahl der eingegangenen Datenpunkte. Das resultierende Rechteck nennen wir das mittlere Abweichungsrechteck. Ein Maß für den Zusammenhang von Lernzeit und Klausurpunkte ist also die Fläche des mittleren Abweichungsrechtecks, s. Abbildung 8.5.

Abbildung 8.5: Die Kovarianz als mittleres Abweichungsrechteck. Die Fläche der Rechtecks entspricht dem Wert der Kovarianz.

8.3.2 Kovarianz

Definition 8.2 (Kovarianz) Die Kovarianz ist definiert als die Fläche des mittleren Abweichungsrechtecks. Sie ist ein Maß für die Stärke und Richtung des linearen Zusammenhangs zweier metrischer Variablen, s. Abbildung 8.5. $◻$

🧑‍🎓 Zu viele Bilder! Ich brauch Zahlen.

🧑‍🏫 Kommen gleich!

Tabelle 8.2 zeigt beispielhaft, wie sich die Kovarianz berechnet. Berechnen wir als Nächstes das mittlere Abweichungsrechteck, die Kovarianz, für die Noten und Lernzeit der vier Studierenden aus Tabelle 8.1. Sie beträgt 162.

Wenn Sie die Werte selber nachrechnen wollen, finden Sie den Noten-Datensatz in der Datei noten.csv.

Tabelle 8.2: Werte der Abweichungsrechtecke. avg: average (Mittelwert), cov_sign: Vorzeichen der Kovarianz,_pos: positiver Wert auf der entsprechenden Achse (x/y), xy_area: Produkt von x_delta und y_delta

id	y	x	x_avg	y_avg	x_delta	y_delta	cov_sign	xy_area
1	72	70	53	51	17	20.8	1	353
2	44	40	53	51	-13	-7.2	1	94
3	39	35	53	51	-18	-12.2	1	220
4	50	67	53	51	14	-1.2	-1	-18

d %>%
  summarise(kovarianz = mean(xy_area))

kovarianz
162

Die Formel der Kovarianz lautet, s. Gleichung 8.1:

$$\begin{array}{}\text{(8.1)}& \text{cov(xy)}=s_{xy}:=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})=\frac{1}{n}\sum _{i=1}^{n}d{x}_i\cdot d{y}_i\end{array}$$

Gleichung 8.1 in Worten ausgedrückt:

1. Rechne für jedes $x_i$ die Abweichung vom Mittelwert, $\overline{x}$, aus, $d{x}_i$.
2. Rechne für jedes $y_i$ die Abweichung vom Mittelwert, $\overline{y}$, aus, $d{y}_i$.
3. Multipliziere für alle $i$ $d{x}_i$ mit $x{y}_i$, um die Abweichungsrechtecke $d{x}_{i}d{y}_i$ zu erhalten.
4. Addiere die Flächen der Abweichungsrechtecke.
5. Teile durch die Anzahl der Beobachtungen $n$.

Beispiel 8.2 (Variablen mit positiver Kovarianz)  

• Größe und Gewicht
• Lernzeit und Klausurerfolg
• Distanz zum Ziel und Reisezeit
• Temperatur und Eisverkauf $◻$

Beispiel 8.3 (Variablen mit negativer Kovarianz)  

• Lernzeit und Freizeit
• Alter und Restlebenszeit
• Temperatur und Schneemenge
• Lebenszufriedenheit und Depressivität$◻$

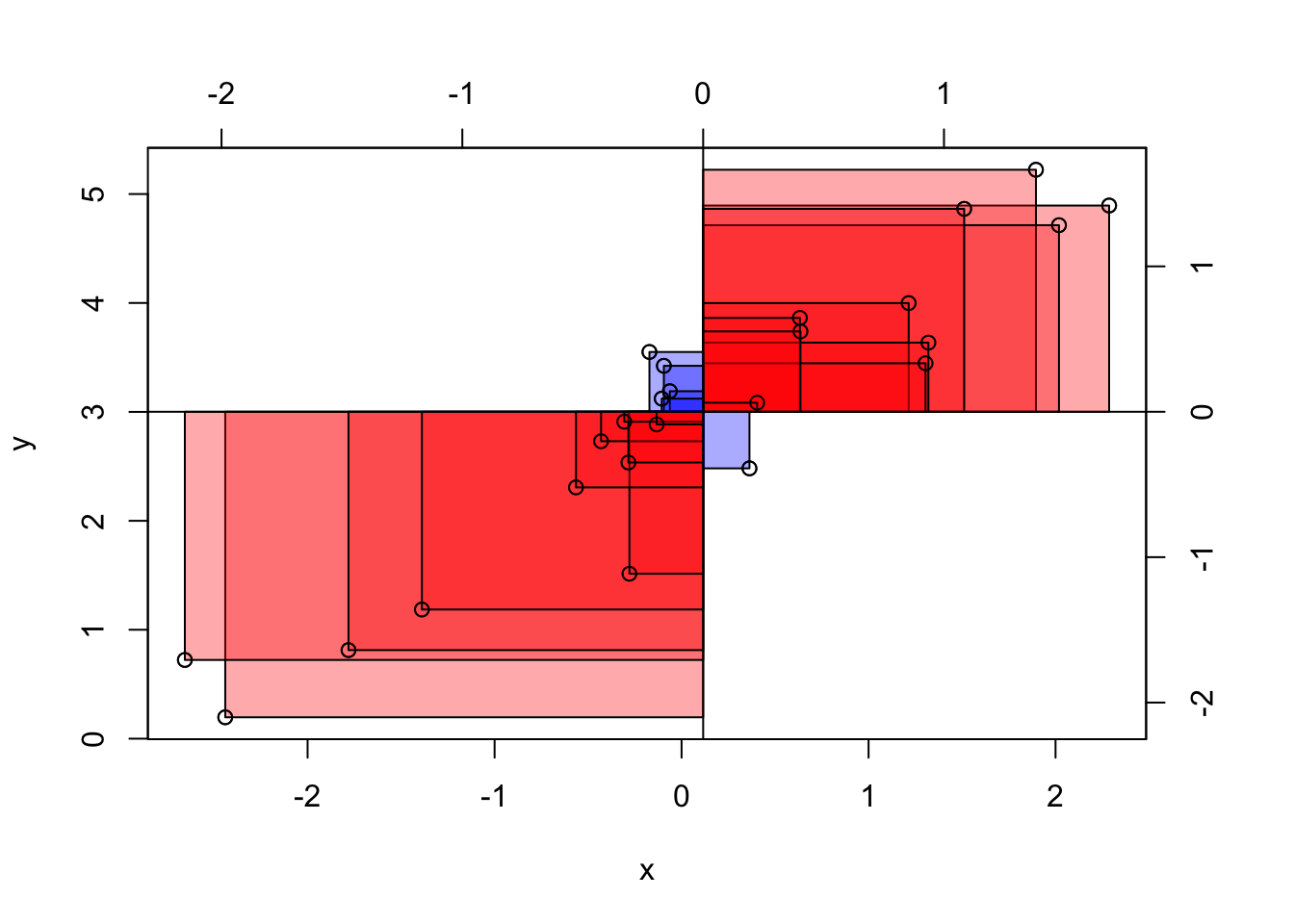
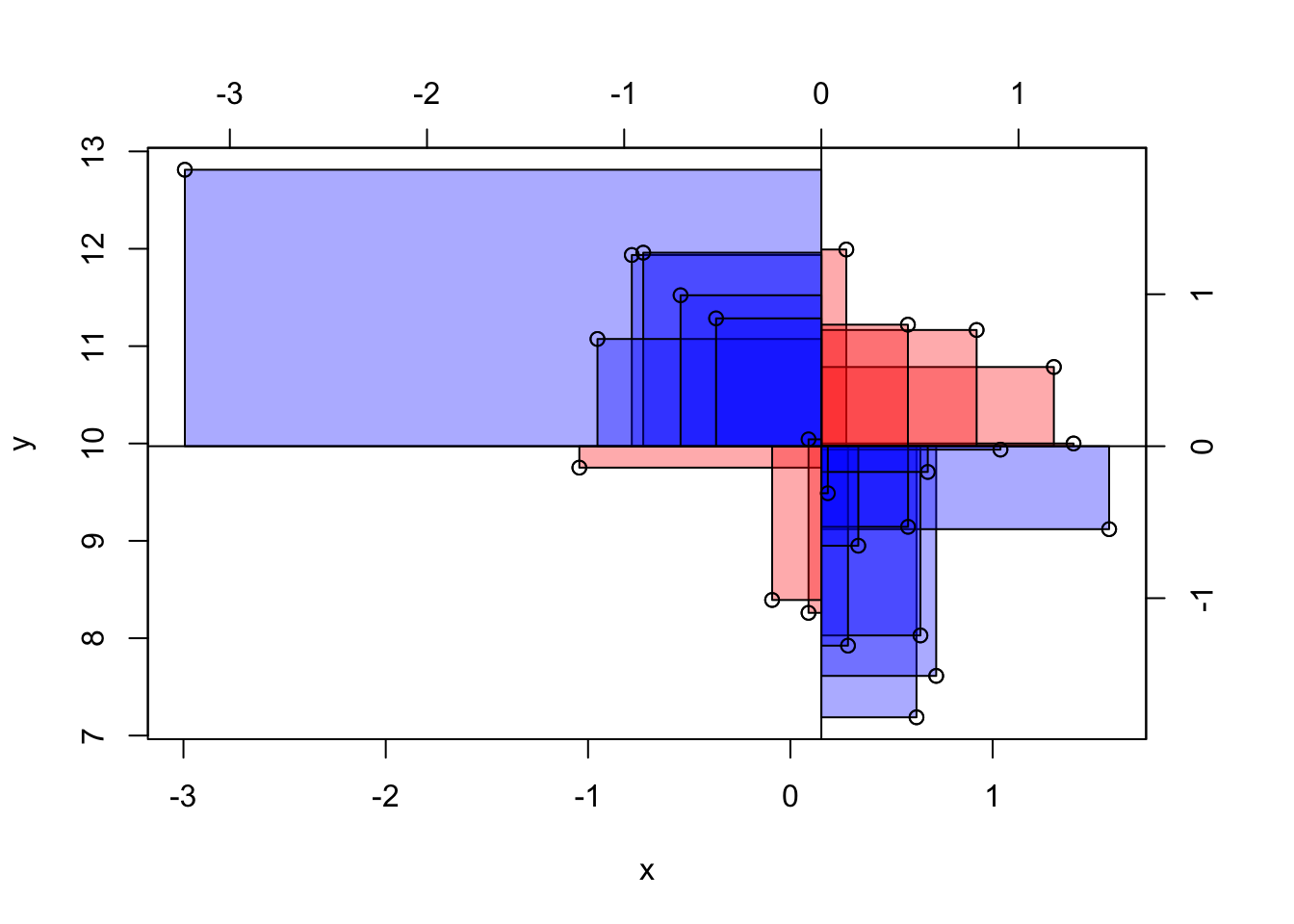
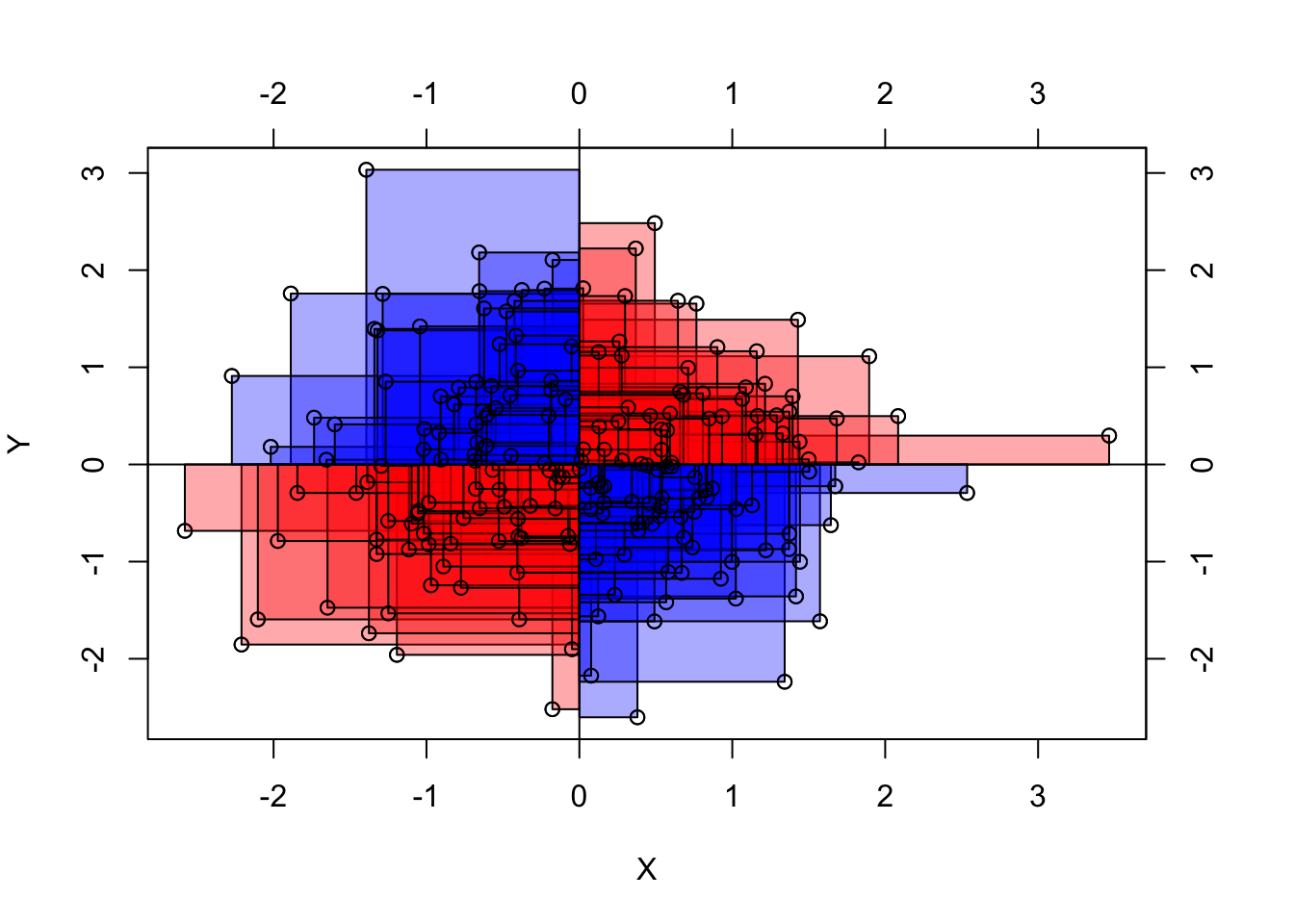
Zwei Extrembeispiele für Kovarianz-Werte sind in Abbildung 8.6 dargestellt.

(a) kein Zusammenhang

 

(b) perfekter (positiver) Zusammenhang

Abbildung 8.6: Verschiedene Werte der Kovarianz

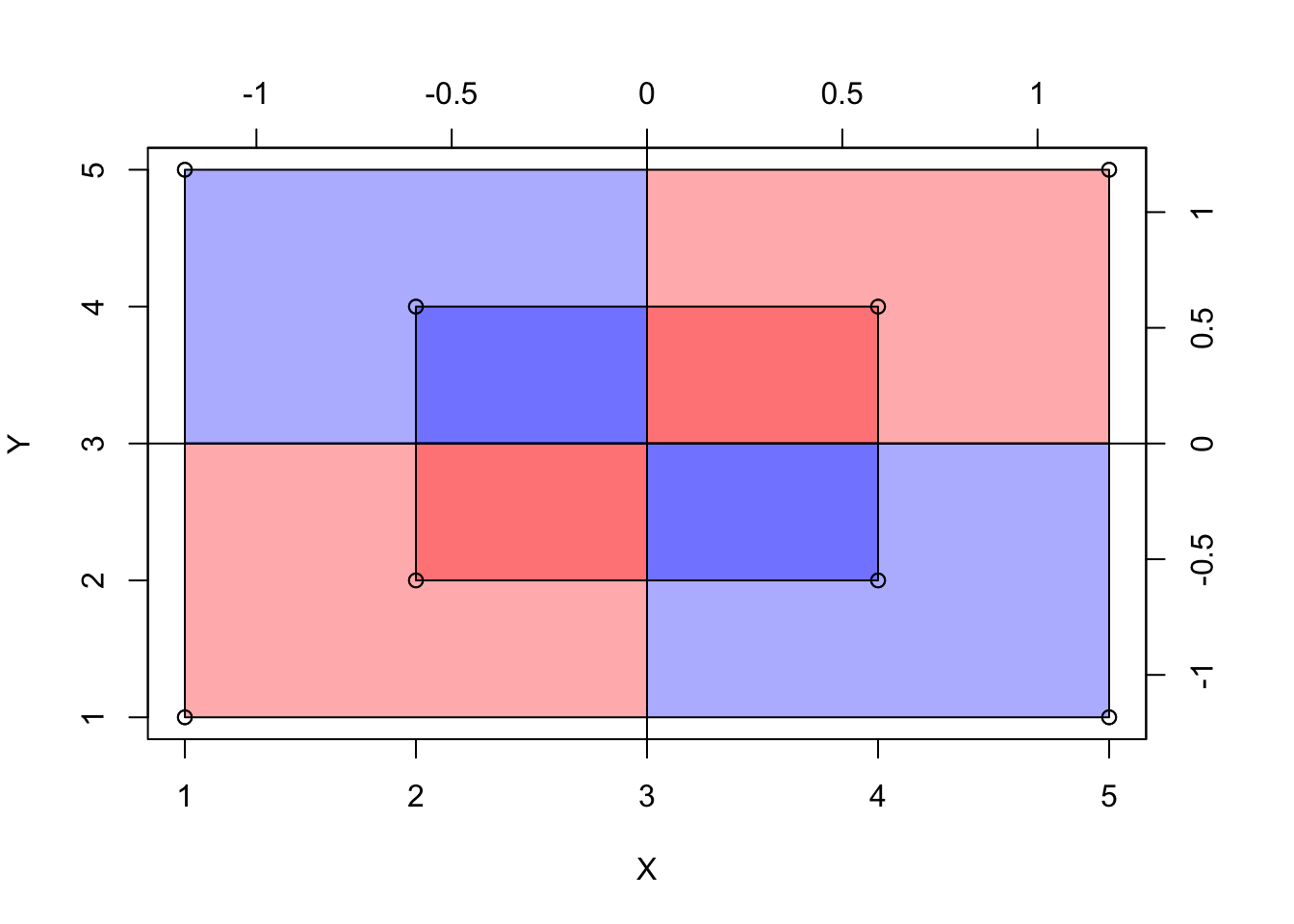
Bei einer Kovarianz von (ungefähr) Null ist die Gesamt-Fläche der Abweichungsrechtecke, wenn man sie pro Quadrant aufsummiert, (ungefähr) gleich groß, s. Abbildung 8.7. Zur Erinnerung: Bei der Varianz waren es Quadrate; bei der Kovarianz sind es jetzt Rechtecke.

Addiert man die Abweichungsrechtecke (unter Beachtung der Vorzeichen), so beträgt die Summe in etwa (bzw. genau) Null. Damit ist die Kovarianz in diesem Fall etwa (bzw. genau) Null, s. Gleichung 8.2: Wenn die Summe der Aweichungsrechtecke Null ist, dann ist auch ihr Mittelwert (MW) Null. Damit ist die Kovarianz Null.

$$\begin{array}{}\text{(8.2)}& \begin{array}{rl}\sum (dX\cdot dY)& =0\\ \iff \text{MW}(dX\cdot dY)& =0\\ \iff \text{cov}(X,Y)& =0\end{array}\end{array}$$

(a) 4 Abweichungsrechtecke

 

(b) 200 Abweichungsrechtecke

Abbildung 8.7: Wenn die Kovarianz 0 ist, gleichen sich die Abweichungsrechtecke auf 0 aus; ihre Fläche addiert zu 0.

8.3.3 Die Kovarianz ist schwer zu interpretieren

Die Kovarianz hat den Nachteil, dass sie abhängig ist von der Skalierung. So steigt die Kovarianz z.$$B. um den Faktor 100, wenn man eine Variable (z.$$B. Einkommen) anstelle von Euro in Cent bemisst. Das ist nicht wünschenswert, denn der Zusammenhang zwischen z.$$B. Einkommen und Lebenszufriedenheit ist unabhängig davon, ob man Einkommen in Euro, Cent oder Dollar misst. Außerdem hat die Kovarianz keinen Maximalwert, der einen perfekten Zusammenhang anzeigt. Insgesamt ist die Kovarianz schwer zu interpretieren und wird in der praktischen Anwendung nur wenig verwendet.

8.4 Korrelation

8.4.1 Korrelation als mittleres z-Produkt

Der Korrelationskoeffizient $r$ nach Karl Pearson (1896) löst das Problem, dass die Kovarianz schwer interpretierbar ist. Der Wertebereich von $r$ reicht von -1 (perfekte negative lineare Korrelation) bis +1 (perfekte positive lineare Korrelation). Eine Korrelation von $r=0$ bedeutet kein linearer Zusammenhang.

Die Korrelation berechnet sich wie folgt:

1. Teile alle $x_i$ durch ihre Standardabweichung, $s_x$
2. Teile alle $y_i$ durch ihre Standardabweichung, $s_y$
3. Berechne mit diesen Werten die Kovarianz

Teilt man nämlich alle $x_i$ bzw. $y_i$ durch ihre Standardabweichung, so führt man mit $X$ bzw. $Y$ eine z-Transformation durch. Daher kann man den Korrelationskoeffizienten $r$ definieren wie in Definition 8.3.

Definition 8.3 (Korrelationskoeffizient $r$) Der Korrelationskoeffizient $r$ (nach Pearson) ist definiert als das mittlere Produkt der z-Wert-Paare, s. Gleichung 8.3, vgl. Cohen et al. (2003). Er ist ein Maß des linearen Zusammenhangs zweier metrischer Variablen. Der Wertebereich ist $[-1;1]$, wobei 0 keinen linearen Zusammenhang anzeigt und $|r|=1$ perfekten linearen Zusammenhang. $◻$

$$\begin{array}{}\text{(8.3)}& r_{xy}=\frac{1}{n}\sum _{i=1}^n{z}_{x_i}{z}_{y_i}\end{array}$$

Man beachte, dass eine Korrelation (genauso wie eine Kovarianz) nur für metrische Variablen definiert ist. Aus dem Korrelationskoeffizienten können Sie zwei Informationen ableiten:

1. Vorzeichen: Ein positives Vorzeichen bedeutet positiver (gleichsinniger) linearer Zusammenhang (und umgekehrt: negatives Vorzeichen, negativer, also gegensinniger linearer Zusammenhang).
2. Absolutwert der Korrelation: Der Absolutwert (Betrag) des Korrelationskoeffizienten gibt die Stärke des linearen Zusammenhangs an. Je näher der Wert bei 1 liegt, desto stärker ist der (lineare) Zusammenhang.

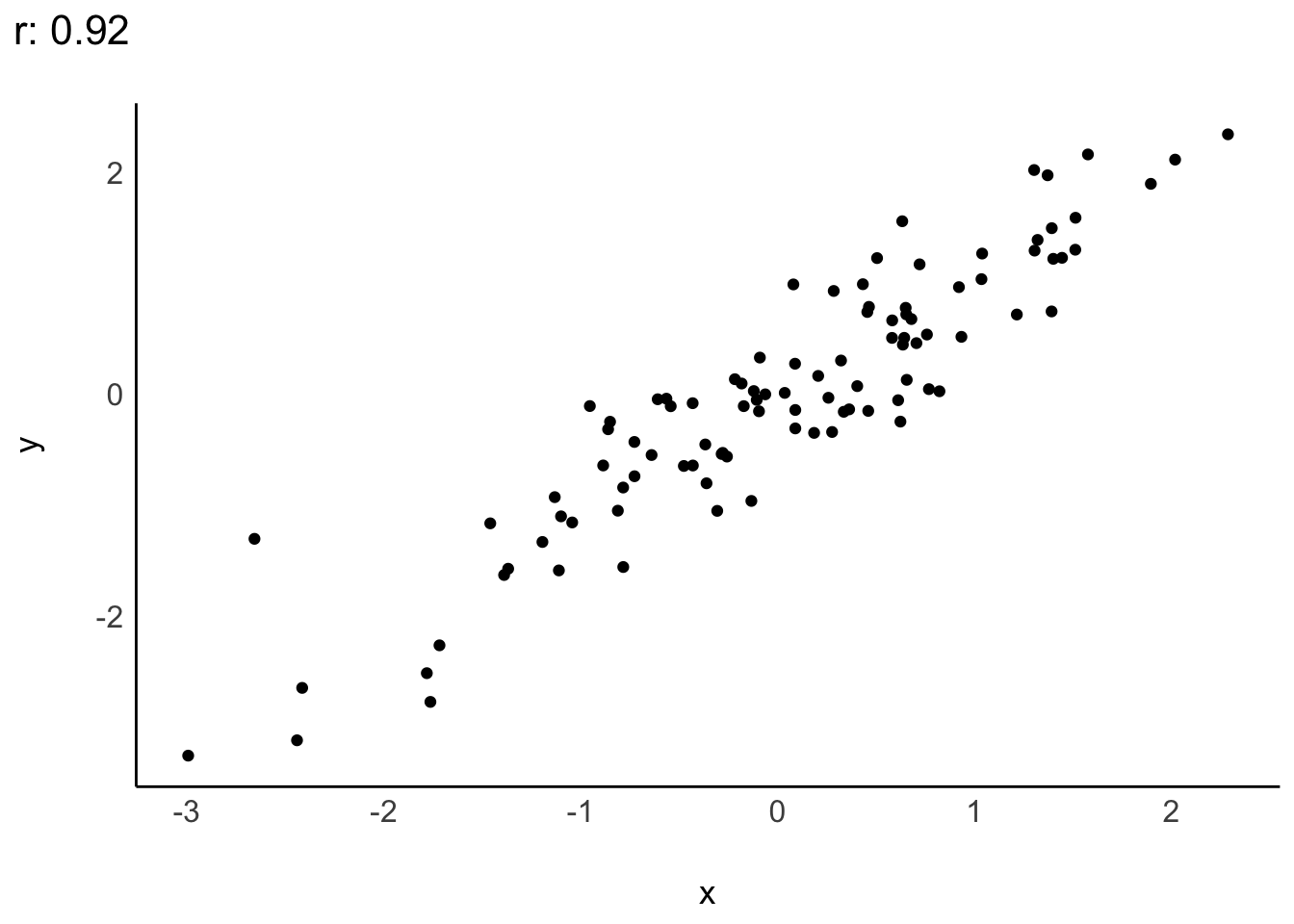
Eine Zuordnung des Korrelationskoeffizienten zum Profil des Streudiagramms zeigt Abbildung 8.8.

Abbildung 8.8: Verschiedene Streudiagramme, die sich in ihrem Korrelationskoeffizienten unterscheiden (DenisBoigelot, 2011)

Die untere Zeile von Abbildung 8.8 zeigt Beispiele für nicht-lineare Zusammenhänge. Wie man sieht, liegt in diesen Beispielen kein linearer Zusammenhang vor ($r=0$), obwohl ein starker nicht-linearer Zusammenhang besteht.

Übungsaufgabe 8.2 (Korrelationsspiel) Spielen Sie das Korrelationsspiel²: Sie Sehen ein Streudiagramm und müssen den richtigen Korrelationskoeffizienten eingeben. $◻$

Übungsaufgabe 8.3 (Interaktive Visualisierung der Korrelation) Auf der Seite von RPsychologist³ findet sich eine ansprechende dynamische Visualisierung der Korrelation. Nutzen Sie sie, um Ihr Gefühl für die Stärke des Korrelationskoeffizienten zu entwickeln. $◻$

8.4.2 Korrelation mit R berechnen

Ob der Verkaufspreis (total_pr) wohl mit der Dauer der Auktion (duration) oder mit der Anzahl der Gebote (n_bids) (linear) zusammenhängt? Schauen wir nach! Die Funktion correlation (aus dem Paket easystats) erledigt das Rechnen für uns, s. Tabelle 8.3.

mariokart |> 
  select(total_pr, duration, n_bids) |> 
  correlation()  |>  # aus `easystats`
  summary()

Tabelle 8.3: Korrelation berechnen mittels der Funktion correlation aus easystats

Parameter	n_bids	duration
total_pr	0.13	-0.04
duration	-0.12

Sie können auch auf die letzte Zeile, also dem Befehl summary verzichten. Dann ist die Ausgabe ausführlicher.

8.4.3 Korrelation ist nicht Kausation

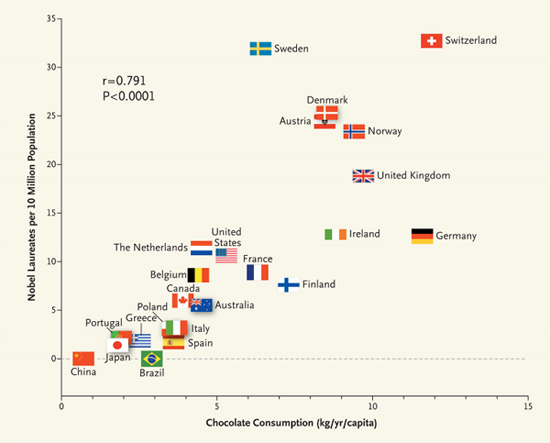
Eine Studie fand eine starke Korrelation zwischen der (Höhe des) Schokoladenkonsums eines Landes und (Anzahl der) Nobelpreise eines Landes (Messerli, 2012), s. Abbildung 8.9.

Abbildung 8.9: Schoki futtern macht schlau? (Messerli, 2012)

Korrelation (bzw. Zusammenhang) ist ungleich Kausation! Korrelation kann bedeuten, dass eine Kausation vorliegt, aber es muss auch nicht sein, dass Kausation vorliegt. Liegt Korrelation ohne Kausation vor, so spricht man von einer Scheinkorrelation.

8.4.4 Korrelation misst nur linearen Zusammenhang

Beispiel 8.4 (Scheinkorrelation: Störche und Babys) Ein Mythos besagt: Die Anzahl der Störche pro Landkreis korreliert mit der Anzahl der Babys in diesem Landkreis (vgl. Matthews, 2000). Eine mögliche Erklärung für dieses (nur scheinbare) Paradoxon ist, dass die “Naturbelassenheit” des Landkreises die gemeinsame Ursache von Störchen ist (Störche lieben Natur) und Babys ist (die Gegebenheiten bei hoher Naturbelassenheit begünstigteine höhere Zahl von Kindern pro Frau). Wir müssen die Erklärung keinesfalls glauben; sie soll das Beispiel nur konkreter machen. Uns geht es hier nur um die Erkennung von Scheinkorrelation. $◻$

Beispiel 8.5 (Glatze macht Corona?) Kahle Männer aufgepasst! Macht eine Glatze krank? Männer mit Glatze bekommen häufiger Corona (Goren et al., 2020): “Bald men at higher risk of severe case of Covid-19, research finds”. Eine alternative Erklärung lautet, dass Alter einen Effekt hat auf Glatze (je älter ein Mann, desto wahrscheinlicher ist es, dass er eine Glatze hat) und auf die Schwere des Corona-Verlaufs (ältere Menschen haben deutlich schwerere Corona-Verläufe). $◻$

8.5 Wie man mit Statistik lügt

8.5.1 Einschränkung der Spannweite

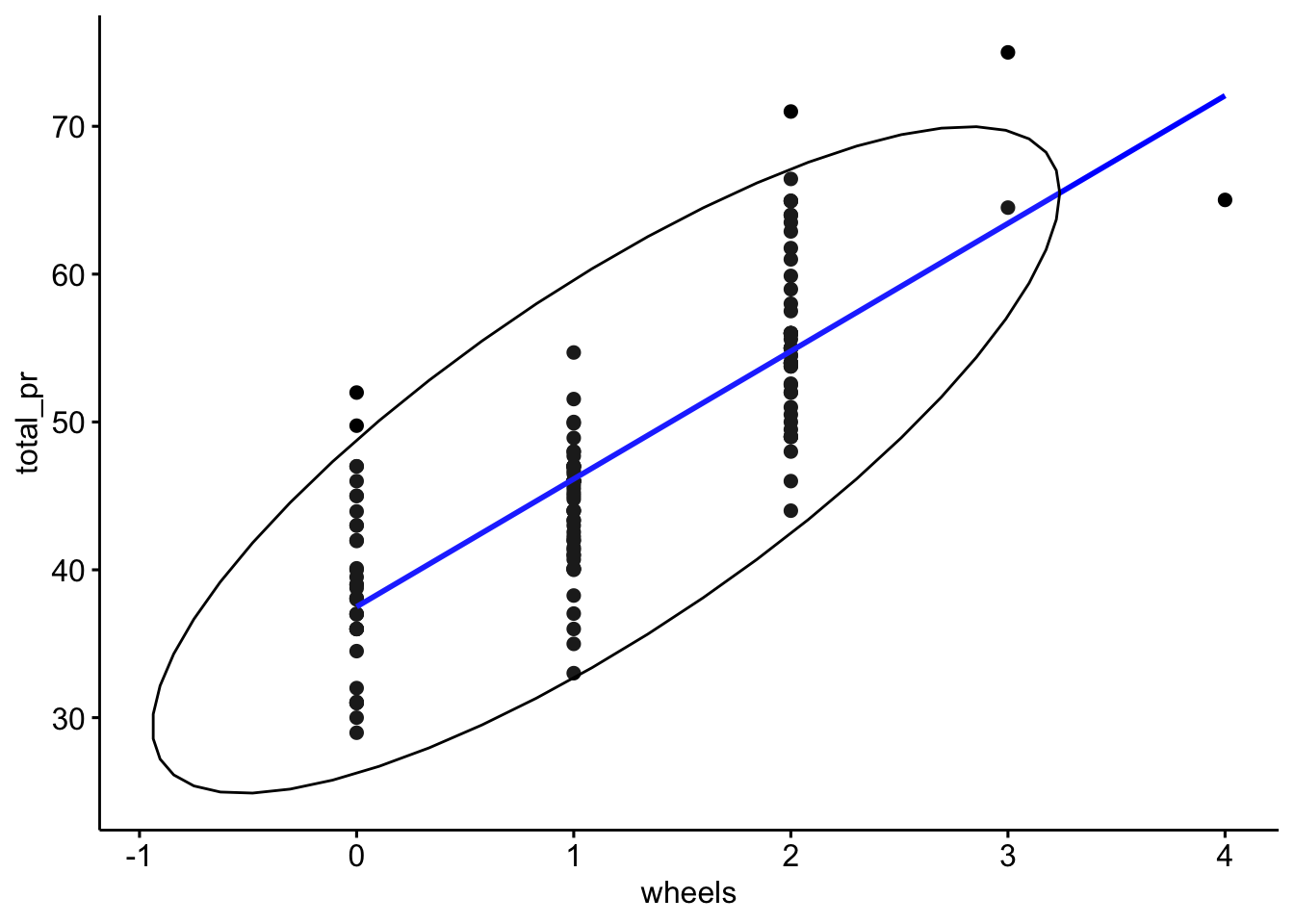
Durch (nicht-randomisierte) Einschränkung (Restriktion) der Spannweite einer (oder beider) Variablen sinkt die Stärke (der Absolutwert) einer Korrelation, vgl. Cohen et al. (2003); s. Abbildung 8.10.

Erstellen wir uns dazu zwei Datensätze mit je zwei Variablen, $X$ und $Y$ und mit Umfang $n=100$. Einer der beiden Datensätze sei mit Einschränkung der Spannweite und einer ohne. $X$ und $Y$ seien normalverteilt mit $\mu =0$ (Mittelwert) und $\sigma =1$ (Streuung); s. Datensatz d in Listing 8.1. Man kann sich mit dem Befehl rnorm(n, m, sd) $n$ normalverteilte Variablen mit Mittelwert $m$ und Streuung $sd$ von R erzeugen lassen. Wir schränken dann den Wertebereich von $X$ ein auf, sagen wir, auf $[-0.5,.5]$ (Datensatz d_filtered), s. Listing 8.1.

Listing 8.1: Korrelation mit eingeschränkter Spannweite

n <- 1e2
d <- tibble(x = rnorm(n = n, mean = 0, sd = 1),
            e = rnorm(n = n, mean = 0, sd = .5),
            y = x + e)

x_min <- -0.5
x_max <- 0.5

d_filtered <-  # Range-Einschränkung:
d |> filter(between(x, x_min, x_max))

(a) Ohne Einschränkung des Range: Starke Korrelation

 

(b) Mit Einschränkung des Range: Schwächere Korrelation

Abbildung 8.10: Schränkt man den Range einer (oder beider) Variablen ein, so sinkt die Stärke der Korrelation

Übungsaufgabe 8.4 (Berechnen Sie die Korrelation) Glauben Sie nicht, prüfen Sie nach! Berechnen Sie die Korrelation von $X$ und $Y$ im Datensatz d und d_filtered! $◻$

8.6 Fallbeispiel

In Ihrer Arbeit beim Online-Auktionshaus analysieren Sie, welche Variablen mit dem Verkaufspreis von Computerspielen zusammenhängen. Falls der Datensatz auf Ihrem Computer (am besten in Ihrem Projektverzeichnis in RStudio) abgelegt ist, können Sie die Daten so (in mittlerweile gewohnter Manier) importieren: mariokart <- read.csv("mariokart.csv") Falls der Datensatz im Unterordner mit Namen “Mein_Unterordner” liegt, so würden Sie folgenden Pfad eingeben: mariokart <- read.csv("Mein_Unterordner/mariokart.csv"). Man beachte, dass solche sog. relativen Pfade, wie Mein_Unterordner/, die relativ zu Ihrem Arbeitsverzeichnis, d.$$h. Ihr Projektverzeichnis in R-Studio, liegen, nicht mit einem Schrägstrich (Slash) beginnen. Falls Sie die Daten nicht auf Ihrem Computer haben, können Sie sie bequem von z.$$B. der Webseite von Vincent Arel-Bundock herunterladen. Den Pfad hatten wir in Listing 1.1 definiert.

mariokart <- read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/openintro/mariokart.csv")

Sie wählen die Variablen von mariokart, die Sie in diesem Fall interessieren – natürlich nur die metrischen – und lassen sich mit cor die Korrelation aller Variablen untereinander ausgeben:

mariokart %>%  
  dplyr::select(duration, n_bids, start_pr, ship_pr, total_pr, seller_rate, wheels) %>% 
  cor() %>% 
  round(2) # Runden auf zwei Dezimalen
##             duration n_bids start_pr ship_pr total_pr seller_rate wheels
## duration        1.00  -0.12     0.13    0.27    -0.04       -0.15  -0.30
## n_bids         -0.12   1.00    -0.63    0.03     0.13       -0.11  -0.08
## start_pr        0.13  -0.63     1.00    0.03     0.07        0.28   0.16
## ship_pr         0.27   0.03     0.03    1.00     0.54       -0.02   0.05
## total_pr       -0.04   0.13     0.07    0.54     1.00        0.01   0.33
## seller_rate    -0.15  -0.11     0.28   -0.02     0.01        1.00  -0.15
## wheels         -0.30  -0.08     0.16    0.05     0.33       -0.15   1.00

Achtung, Namensverwechslung! Es kann vorkommen, dass Sie zwei R-Pakete geladen haben, in denen es jeweils z.$$B. eine Funktion mit Namen select gibt. R wird in dem Fall diejenige Funktion verwenden, deren Paket Sie als letztes gestartet haben. Das kann dann das falsche select sein. In dem Fall resultiert eine verwirrende Fehlermeldung, die sinngemäß sagt: “Hey Mensch, du hast Argumente in der Funktion verwendet, die du gar nicht verwenden darfst, da es sie nicht gibt.” Auf Errisch: Error in select(., duration, n_bids, start_pr, ship_pr, total_pr, seller_rate, : unused arguments (duration, n_bids, start_pr, ship_pr, total_pr, seller_rate, wheels). Eine einfache Abhilfe ist es, R zu sagen: “Hey R, nimm gefälligst select aus dem Paket dplyr, dort”wohnt” nämlich select. Auf Errisch spricht sich das so: dplyr::select(...).

Etwas schöner sieht die Ausgabe mit dem Befehl correlation aus easystats aus, s. Tabelle 8.4.

mariokart %>% 
  dplyr::select(duration, n_bids, start_pr, ship_pr, total_pr, seller_rate, wheels) |> 
  correlation() |> 
  summary()

Tabelle 8.4: Korrelationstabelle (tidy) im Datensatz mariokart

Parameter	wheels	seller_rate	total_pr	ship_pr	start_pr	n_bids
duration	-0.30**	-0.15	-0.04	0.27*	0.13	-0.12
n_bids	-0.08	-0.11	0.13	0.03	-0.63***
start_pr	0.16	0.28*	0.07	0.03
ship_pr	0.05	-0.02	0.54***
total_pr	0.33**	0.01
seller_rate	-0.15

Die Sternchen in Tabelle 8.4 geben die sog. statistische Signifikanz der Korrelation an; ein Thema, das wir einfach gekonnt ignorieren.

Möchte man nur einzelne Korrelationskoeffizienten ausrechnen, können wir die Idee des Zusammenfassens, s. Abbildung 8.1, nutzen: mariokart %>% summarise(korrelation = cor(total_pr, wheels)).

Im Falle von fehlenden Werte müssen Sie den Befehl cor aus seiner schüchternen Vorsicht befreien und ermutigen, trotz fehlender Werte einen Korrelationskoeffizienten auszugeben. Das geht mit dem Argument use = "complete.obs" in cor.

mariokart %>% 
  summarise(cor_super_wichtig = cor(total_pr, wheels, use = "complete.obs"))

🧑‍🎓 Immer so viele Zahlen! Ich brauch Bilder.

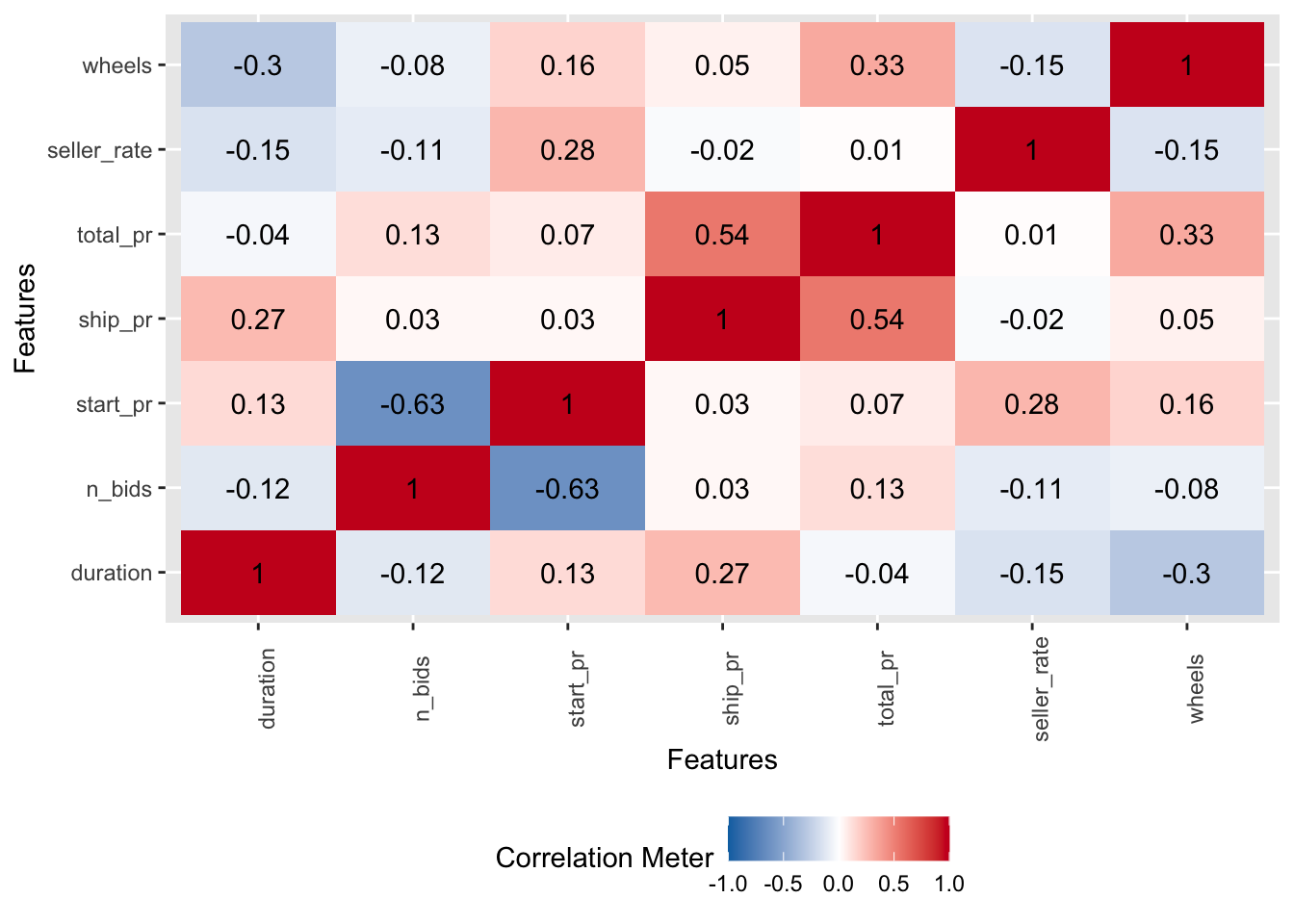
Mit dem Befehl plot_correlation aus dem R-Paket dataExplorer bekommt man eine ansehnliche Heatmap zur Verdeutlichung der Korrelationswerte, s. Abbildung 8.11.

library(DataExplorer)

mariokart %>% 
  dplyr::select(duration, n_bids, start_pr, ship_pr, total_pr, seller_rate, wheels) %>% 
  plot_correlation()

Abbildung 8.11: Heatmap zu den Korrelationen im Datensatz mariokart.

8.7 Aufgaben

Schauen Sie sich auch mal auf der Webseite Datenwerk⁴ die Aufgaben zu dem Tag association an.

1. nasa02
2. mariokart-korr1
3. mariokart-korr2
4. mariokart-korr3
5. mariokart-korr4
6. korr01
7. korr02

Testen Sie Ihr Wissen mit einem Quiz zur deskriptiven Statistik (Maße der zentralen Tendenz, Variabilität, Verteilungsformen, Normalverteilung, Korrelation).

8.8 Fallstudien

Bitte verstehen Sie die folgenden Fallstudien als eine Auswahl. Es ist nicht nötig, dass Sie alle Fallstudien bearbeiten. Sehen Sie die Fallstudien eher als Angebot zur selektiven Vertiefung und Übung, dort, wo Sie es nötig haben.

1. YACSDA: EDA zu Flugverspätungen⁵ im Datenwerk unter dem Tag flights-yacsda-eda zu finden.

Hinweis

Einige der Fallstudien oder Übungsaufgaben können theoretische Inhalte (Konzepte der Statistik) oder praktische Inhalte (R-Befehle) enthalten, die Sie (noch) nicht kennen. In dem Fall: Einfach ignorieren. Oder Sie suchen nach einer Lösung anhand von Konzepten bzw. R-Befehlen, die Sie kennen. $◻$

2. YACSDA: Topgear⁶
3. Datensatz flights: Finde den Tag mit den meisten Abflügen⁷
4. Tidyverse Case Study: Exploring the Billboard Charts⁸

8.9 Literaturhinweise

Auch die Korrelation ist ein Allzeit-Favorit in der Statistik; entsprechend wird Ihnen jedes typische Statistik-Buch die Grundlagen erläutern. Schauen Sie doch mal, was Ihre Bibliothek Ihnen zu bieten hat. Wer eine unorthodoxe (geometrische!) Herangehensweise an die Korrelation (und Regression) sucht, darf sich auf eine Menge Aha-Momente bei Kaplan (2009) freuen. Ein schönes, modernes Statistikbuch bietet Poldrack (2023); auch dieses Buch ist frei online verfügbar. Tipp: Nutzen Sie die Übersetzungfunktion Ihres Browsers, wenn Sie das Buch nicht in Englisch lesen wollen. Ein Klassiker, wenn auch nicht mehr ganz frisch, ist Cohen et al. (2003); immer noch sehr empfehlenswert, aber etwas höheren Anspruchs. Was ist Scheinkorrelation und was ist “echte” Korrelation? Dieser Unterschied – der für die Wissenschaft zentral ist – wird von Pearl & Mackenzie (2018) auf entspannte Art erläutert; nebenbei lernt man einiges zur Geschichte der Wissenshaft.

Hier finden Sie weitere Beispiele für Scheinkorrelationen. Dieser TED-Vortrag informiert zum Thema Scheinkorrelation.

Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd Ed. Lawrence Erlbaum.

DenisBoigelot. (2011). English: Redesign File:Correlation_examples.Png Using Vector Graphics (SVG File) [Artwork]. https://commons.wikimedia.org/w/index.php?curid=15165296

Goren, A., Vaño-Galván, S., Wambier, C. G., McCoy, J., Gomez-Zubiaur, A., Moreno-Arrones, O. M., Shapiro, J., Sinclair, R. D., Gold, M. H., Kovacevic, M., Mesinkovska, N. A., Goldust, M., & Washenik, K. (2020). A Preliminary Observation: Male Pattern Hair Loss among Hospitalized COVID-19 Patients in Spain – A Potential Clue to the Role of Androgens in COVID-19 Severity. Journal of Cosmetic Dermatology, 19(7), 1545–1547. https://doi.org/10.1111/jocd.13443

Kaplan, D. T. (2009). Statistical Modeling: A Fresh Approach. CreateSpace. https://dtkaplan.github.io/SM2-bookdown/

Matthews, R. (2000). Storks Deliver Babies (P= 0.008). Teaching Statistics, 22(2), 36–38. https://doi.org/10.1111/1467-9639.00013

Messerli, F. H. (2012). Chocolate Consumption, Cognitive Function, and Nobel Laureates. New England Journal of Medicine, 367(16), 1562–1564. https://doi.org/10.1056/NEJMon1211064

Pearl, J., & Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. Basic Books.

Pearson, K. (1896). VII. Mathematical Contributions to the Theory of Evolution.—III. Regression, Heredity, and Panmixia. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 187, 253–318. https://doi.org/10.1098/rsta.1896.0007

Poldrack, R. A. (2023). Statistical Thinking: Analyzing Data in an Uncertain World. Princeton University Press. https://statsthinking21.github.io/statsthinking21-core-site/

---

1. 🧑‍🎓 Typisches Lehrerbeispiel!

2. https://gallery.shinyapps.io/correlation_game/

3. https://rpsychologist.com/correlation/

4. https://sebastiansauer.github.io/Datenwerk/

5. https://sebastiansauer.github.io/Datenwerk/posts/flights-yacsda-eda

6. https://data-se.netlify.app/2021/02/11/yacda-topgear/

7. https://data-se.netlify.app/2021/05/27/datensatz-flights-finde-den-tag-mit-den-meisten-abfl%C3%BCgen/

8. https://www.njtierney.com/post/2017/11/07/tidyverse-billboard/